题目内容
已知函数 .
.
(Ⅰ)设函数 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列 ,求证:
,求证: 为等差数列;
为等差数列;
(Ⅱ)设函数 的图像的顶点到
的图像的顶点到 轴的距离构成数列
轴的距离构成数列 ,求
,求 的前
的前 项和
项和 .
.
(1)根据等差数列的定义来证明,结合函数的将诶西施,得到其通项公式即可证明。
(2)
解析试题分析:解:(Ⅰ)∵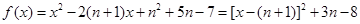 ,
,
∴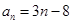 , 2分
, 2分
∴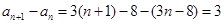 ,
,
∴数列 为等差数列. 4分
为等差数列. 4分
(Ⅱ)由题意知, , 6分
, 6分
∴当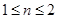 时,
时,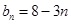 ,
,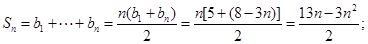 8分
8分
当 时,
时,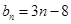 ,
,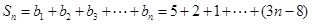
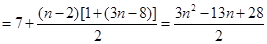 . 10分
. 10分
∴ . 12分
. 12分
考点:等差数列,等比数列
点评:解决的关键是根据利用函数为背景得到数列的通项公式,然后借助于等比数列的求和公式求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 }的前
}的前 项和为
项和为 (
( 为常数,
为常数, N*).
N*). ,
, ,
, ;
; ,若
,若 对任意的正整数
对任意的正整数 的取值范围.
的取值范围. 的前
的前 项和为
项和为 ,
, 
 ,求
,求 ;
;  ,求
,求 的前6项和
的前6项和 ;
; ,证明
,证明 是等差数列.
是等差数列. 满足
满足 ,
, 。
。 项和
项和 及使得
及使得 的前
的前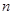 项和为
项和为 ,若
,若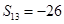 ,
,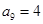 ,求:
,求: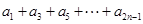 .
. }是等差数列,
}是等差数列, ,
, 时,若自然数
时,若自然数 满足
满足 ,使得
,使得 成等比数列,(1)求数列{
成等比数列,(1)求数列{ 的通项公式及其前n项的和
的通项公式及其前n项的和 的前
的前 项和
项和 ,求数列
,求数列 (n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;