题目内容
已知数列 的前
的前 项和
项和 ,求数列
,求数列 成等差数列的充要条件.
成等差数列的充要条件.
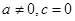
解析试题分析:当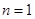 时,
时,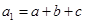 ;当
;当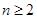 时,
时,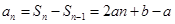
由于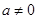 ,∴当
,∴当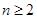 时,
时, 是公差为
是公差为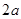 等差数列。
等差数列。
要使 是等差数列,则
是等差数列,则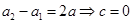 .
.
即 是等差数列的必要条件是:
是等差数列的必要条件是: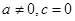 .
.
充分性:
当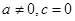 时,
时,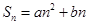 .
.
当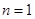 时,
时,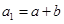 ;当
;当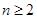 时,
时,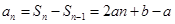 ,
,
显然当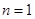 时也满足上式,∴
时也满足上式,∴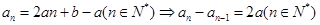
∴ 是等差数列.
是等差数列.
综上可知,数列 是等差数列的充要条件是:
是等差数列的充要条件是: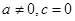
考点:等差数列的判定
点评:判定数列是等差数列一般依据等差数列的定义,判定任意相邻两项的差是否是同意常数即看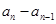 是否是同一常数,若是,则数列是等差数列,若不是,则数列不是等差数列,因此先要由
是否是同一常数,若是,则数列是等差数列,若不是,则数列不是等差数列,因此先要由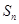 求
求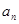 ,此时与注意分
,此时与注意分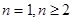 两种情况
两种情况

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,
,
 .
. 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列 ,求证:
,求证: 轴的距离构成数列
轴的距离构成数列 ,求
,求 的前
的前 项和
项和 .
. 是一个等差数列,
是一个等差数列,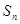 是其前
是其前 项和,且
项和,且 ,
, .
.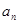 ;
; 的前10项的和
的前10项的和
 满足
满足
 。
。 ,
,  为
为 项和,求
项和,求 。
。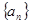 的首项为
的首项为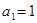 ,其前
,其前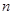 项和为
项和为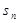 ,且对任意正整数
,且对任意正整数 、
、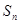 成等差数列.
成等差数列.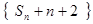 成等比数列;
成等比数列;  中,
中, ,
, ,且
,且
 .
. ,求
,求 是的通项公式;
是的通项公式; 是
是 与
与 的等差中项,求
的等差中项,求 的值,并证明:对任意的
的值,并证明:对任意的 ,
, 是
是 与
与 的等差中项.
的等差中项. 是等差数列,其中
是等差数列,其中 [来]
[来] 值。]
值。]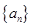 是等差数列,其前n项和公式为
是等差数列,其前n项和公式为 ,
,
 的值;
的值;