题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(1)连接BC1交B1C于点E,连接DE,证明DE∥![]() ,即可证明
,即可证明![]() ∥平面
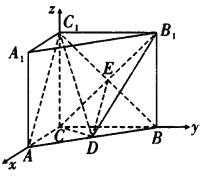
∥平面![]() .(2)以CA,CB,CC1为x轴、y轴、z轴建立如图所示的空间直角坐标系C﹣xyz,直线DC1与平面B1CD所成角为θ,求出平面B1CD的法向量,然后利用空间向量的数量积求解即可.
.(2)以CA,CB,CC1为x轴、y轴、z轴建立如图所示的空间直角坐标系C﹣xyz,直线DC1与平面B1CD所成角为θ,求出平面B1CD的法向量,然后利用空间向量的数量积求解即可.
(Ⅰ)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴点![]() 是
是![]() 的中点,
的中点,
又点![]() 为
为![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() .
.
又DE平面B1CD,AC1平面B1CD,
∴![]() 平面
平面![]() .
.
(Ⅱ)由![]() ,
,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() 可得
可得![]() ,
,
以点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,![]() ,
,
即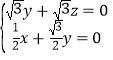 ,令
,令![]() ,得
,得![]() ,
,
∴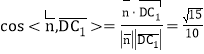 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的质量(单位:克),质量值落在(495,510]的产品为合格品,否则为不合格品.表是甲流水线样本频数分布表,图是乙流水线样本频率分布直方图.

表甲流水线样本频数分布表
产品质量/克 | 频数 |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |
(1)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(2)由以上统计数据作出2×2列联表,并回答能否有95%的把握认为“产品的包装质量与两条自动包装流水线的选择有关”
χ2![]()
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
