题目内容
 (2013•蓟县二模)如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=2BP=4,PC=1,MN=6,则MC的长为
(2013•蓟县二模)如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=2BP=4,PC=1,MN=6,则MC的长为3
3
.分析:先根据相交弦定理求出PC,得到MD,再结合切割线定理即可求出MN的长.
解答:解:AP=2BP=4,PC=1,MN=6,
由相交弦定理得:AP•PB=PC•PD⇒PD=8⇒MD=MC+PC+PD=MC+9.
由切割线定理得:MN2=MC•MD,可得36=MC•(MC+9)⇒MN=3.
故答案为:3.
由相交弦定理得:AP•PB=PC•PD⇒PD=8⇒MD=MC+PC+PD=MC+9.
由切割线定理得:MN2=MC•MD,可得36=MC•(MC+9)⇒MN=3.
故答案为:3.
点评:本题主要考查与圆有关的比例线段以及相交弦定理和切割线定理的应用,是对基础知识的考查,属于基础题.解决这类问题,需要对圆中的有关结论熟悉.

练习册系列答案
相关题目
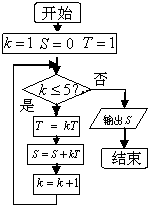 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )