题目内容
已知函数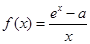 ,
,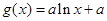 .
.
①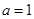 时,求
时,求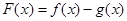 的单调区间;
的单调区间;
②若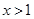 时,函数
时,函数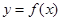 的图象总在函数
的图象总在函数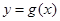 的图象的上方,求实数
的图象的上方,求实数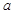 的取值范围.
的取值范围.
.解:(1)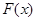 的单增区间为
的单增区间为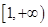 ;单减区间为
;单减区间为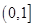 .
.
(2)实数a的取值范围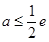
解析

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
已知函数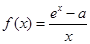 ,
,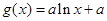 .
.
①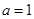 时,求
时,求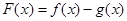 的单调区间;
的单调区间;
②若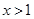 时,函数
时,函数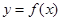 的图象总在函数
的图象总在函数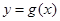 的图象的上方,求实数
的图象的上方,求实数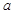 的取值范围.
的取值范围.
.解:(1)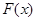 的单增区间为
的单增区间为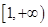 ;单减区间为
;单减区间为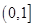 .
.
(2)实数a的取值范围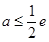
解析

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案