题目内容
(本小题满分12分)
设函数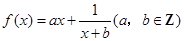 ,曲线
,曲线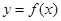 在点
在点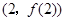 处的切线方程
处的切线方程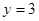 .
.
(1)求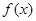 的解析式,并判断函数
的解析式,并判断函数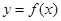 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
(2)证明:曲线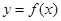 上任一点的切线与直线
上任一点的切线与直线 和直线
和直线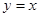 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
(3) 将函数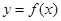 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线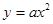 (
(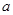 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)
(1) 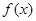 的图像是以点
的图像是以点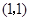 为中心的中心对称图形.
为中心的中心对称图形.
(2) 三角形的面积为定值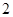
(3) 由三次函数的图象是连续的可知F(x)至少有一零点 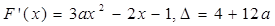
当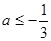 时
时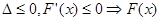 在R上为减函数(减函数至多有一个零点),
在R上为减函数(减函数至多有一个零点),
所以此时F(x)有且只有一个零点;
解析试题分析:解:(1)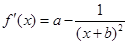 ,
,
曲线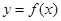 在点
在点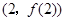 处的切线方程为y=3,
处的切线方程为y=3,
于是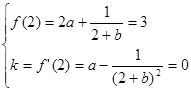 解得
解得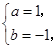 或
或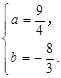
因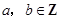 ,故
,故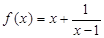 .
. 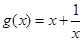 ,满足
,满足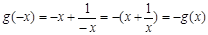 ,所以
,所以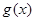 是奇函数
是奇函数
所以,其图像是以原点(0,0)为中心的中心对称图形.
而函数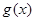 的图像按向量
的图像按向量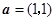 平移,即得到函数
平移,即得到函数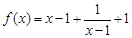 的图像,
的图像,
故函数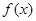 的图像是以点
的图像是以点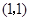 为中心的中心对称图形.
为中心的中心对称图形.
(2)证明:在曲线上任取一点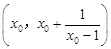 . 由
. 由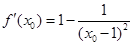 知,
知,
过此点的切线方程为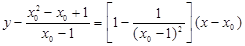 .
.
令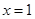 得
得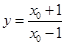 ,切线与直线
,切线与直线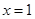 交点为
交点为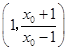 .
.
令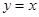 得
得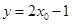 ,切线与直线
,切线与直线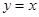 交点为
交点为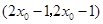 .
.
直线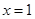 与直线
与直线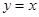 的交点为
的交点为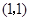 .
.
从而所围三角形的面积为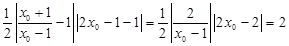 .
.
所以,所围三角形的面积为定值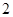 .
.
(3)将函数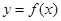 的图象向左平移一个单位后得到的函数为
的图象向左平移一个单位后得到的函数为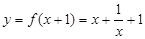 ,
,
它与抛物线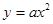 的交点个数等于方程
的交点个数等于方程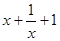 =
=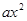 的解的个数
的解的个数
法一:
即 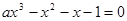 (
(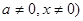 解的个数,(易知0不是其解,不产生增根)
解的个数,(易知0不是其解,不产生增根)
即 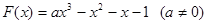 的零点(与x轴交点的横坐标)的个数
的零点(与x轴交点的横坐标)的个数 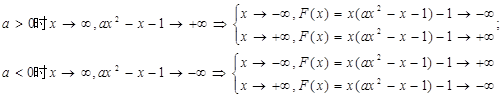
由三次函数的图象是连续的可知F(x)至少有一零点 11分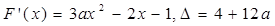
当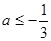 时
时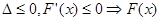 在R上为减函数(减函数至多有一个零点),
在R上为减函数(减函数至多有一个零点),
所以此时F(x)有且只有一个零点;
考点:导数的几何意义以及函数零点
点评:解决的关键是能结合导数的几何意义表示切线方程,进而分析函数的零点个数,需要对于a分类讨论得到,属于中档题。

 阅读快车系列答案
阅读快车系列答案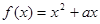 ,且对任意的实数
,且对任意的实数 都有
都有 成立.
成立. 的值;
的值; 在区间
在区间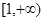 上是增函数.
上是增函数.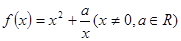
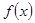 的奇偶性;
的奇偶性;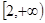 是增函数,求实数
是增函数,求实数 的取值范围。
的取值范围。
 的最小正周期.
的最小正周期. 时,求函数
时,求函数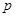 与死亡年数
与死亡年数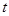 之间的函数关系式;
之间的函数关系式; )
)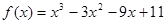
 的递减区间;
的递减区间;
 的不等式
的不等式 ;
; 的图象恒在函数
的图象恒在函数 图象的上方(没有公共点),求
图象的上方(没有公共点),求 的取值范围。
的取值范围。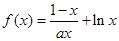
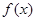 在
在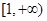 上为增函数,求正实数
上为增函数,求正实数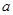 的取值范围;
的取值范围;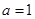 时,求
时,求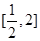 上的最大值和最小值;
上的最大值和最小值;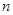 ,都有
,都有 。
。 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值;