题目内容
已知关于x的一次函数y=mx+n.
(Ⅰ)设集合P={-2,-1,1,2,3}和Q={-3,2},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是增函数的概率;
(Ⅱ)实数m,n,满足条件
,求函数y=mx+n在R单调递增,且函数图象经过第二象限的概率.
(Ⅰ)设集合P={-2,-1,1,2,3}和Q={-3,2},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是增函数的概率;
(Ⅱ)实数m,n,满足条件
|
分析:(1)根据古典概率的概率公式求出基本事件的个数即可求出概率.
(2)根据集合概型的概率的公式即可求出对应的概率.
(2)根据集合概型的概率的公式即可求出对应的概率.
解答: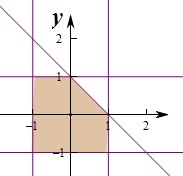 解:(Ⅰ)抽取的全部结果的基本事件有:
解:(Ⅰ)抽取的全部结果的基本事件有:
(-2,-2),(-2,3),(-1,-2),(-1,3),(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共10个基本事件,
设使“函数为增函数”的事件为A,
则A包含的基本事件有:(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共6个基本事件,
∴P(A)=
=
.
(Ⅱ)m,n满足条件
,依题意可得,m>0,n>0,
故点(m,n)的区域为第一象限的阴影部分,
∴所求事件的概率为P=
=
.
 解:(Ⅰ)抽取的全部结果的基本事件有:
解:(Ⅰ)抽取的全部结果的基本事件有:(-2,-2),(-2,3),(-1,-2),(-1,3),(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共10个基本事件,
设使“函数为增函数”的事件为A,
则A包含的基本事件有:(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3),共6个基本事件,
∴P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
(Ⅱ)m,n满足条件
|
故点(m,n)的区域为第一象限的阴影部分,
∴所求事件的概率为P=
| ||
|
| 1 |
| 7 |
点评:本题主要考查古典概型和几何概型的概率求法,要求熟练掌握相应的概率公式,考查学生的计算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目