题目内容
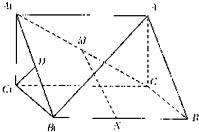 如图,直三棱柱ABC-A1B1C1的底面积是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=
如图,直三棱柱ABC-A1B1C1的底面积是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=| 2 |
(I)证明:MN∥平面ABC;
(II)求A1到平面AB1C1的距离
(III)求二面角A1-AB1-C1的大小.
分析:(I) 取AC中点F,连接MF,BF,证明四边形MNBF为平行四边形,则可证行线面平行的判定定理成立的条件.
(II)设A1到平面AB1C1的距离为h,从题设条件知道,本小题宜用等体积法求解.
(III)三棱柱ABC-A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,又点D是等腰直角三角形A1B1C1斜边A1B1的中点,故有C1D⊥平面A1B1BA,再由作二面角平面角的作法作出平面角,此角所在三角形是直角三角形,在此直角三角形中求该角的三角函数值再由值求角.
(II)设A1到平面AB1C1的距离为h,从题设条件知道,本小题宜用等体积法求解.
(III)三棱柱ABC-A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,又点D是等腰直角三角形A1B1C1斜边A1B1的中点,故有C1D⊥平面A1B1BA,再由作二面角平面角的作法作出平面角,此角所在三角形是直角三角形,在此直角三角形中求该角的三角函数值再由值求角.
解答: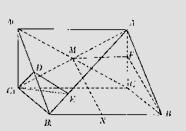 解:(I)证明:取AC中点F,连接MF,BF,
解:(I)证明:取AC中点F,连接MF,BF,
在三角形AC1C中,MN∥C1C且MF=
C1C,BN∥C1C且BN=
C1C,
∴MF∥BN且MF=BN
∴四边形MNBF为平行四边形
∴BF∥MN
∵BF?平面ABC
MN?平面ABC不成立
∴MN∥平面ABC(6分)
(II)设A1到平面AB1C1的距离为h,AA1⊥平面A1B1C1
∴VA1-AB1C1=VA-A1B1C1
∴
S△AB1C1•h=
S△A1B1C1•A1A
∵S△AB1C1=
B1C1•AC1=
×1×
=
,
S△A1B1C1=
B1C1•A1C1=
,AA1=
∴h=
•A1A=
. (10分)
(III)三棱柱ABC-A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,
又点D是等腰直角三角形A1B1C1斜边A1B1的中点.
则C1D⊥A1B1
所以,C1D⊥平面A1B1BA;
平面A1B1BA内,过D作DE⊥AB1,垂足为E,连接C1E,则C1E⊥AB1;
∴∠C1ED是二面角,A1-AB1-C1的平面角,
在Rt△DEC1中,tan∠C1ED=
=
=
,∠C1ED=arctan
所以,二面角,A1-AB1-C1的大小为arctan
.(13分)
 解:(I)证明:取AC中点F,连接MF,BF,
解:(I)证明:取AC中点F,连接MF,BF,在三角形AC1C中,MN∥C1C且MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴MF∥BN且MF=BN
∴四边形MNBF为平行四边形
∴BF∥MN
∵BF?平面ABC
MN?平面ABC不成立
∴MN∥平面ABC(6分)
(II)设A1到平面AB1C1的距离为h,AA1⊥平面A1B1C1
∴VA1-AB1C1=VA-A1B1C1
∴
| 1 |
| 3 |
| 1 |
| 3 |
∵S△AB1C1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
S△A1B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴h=
| S△A1B1C1 |
| S△AB1C1 |
| ||
| 3 |
(III)三棱柱ABC-A1B1C1是直三棱柱,平面ABB1A1⊥平面A1B1C1,
又点D是等腰直角三角形A1B1C1斜边A1B1的中点.
则C1D⊥A1B1
所以,C1D⊥平面A1B1BA;
平面A1B1BA内,过D作DE⊥AB1,垂足为E,连接C1E,则C1E⊥AB1;
∴∠C1ED是二面角,A1-AB1-C1的平面角,
在Rt△DEC1中,tan∠C1ED=
| C1D |
| DE |
| ||||
|
| 2 |
| 2, |
所以,二面角,A1-AB1-C1的大小为arctan
| 2 |
点评:考查线面平行的判定定理,以及点到面的距离的求法,二面角的求法,本题设及知识面广,方法选择灵活,是立体几何中的一道少见的好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.