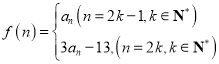题目内容
【题目】已知函数![]() =
=![]() ,其中a>0,且a≠1
,其中a>0,且a≠1
(1)判断![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)若关于![]() 的不等式
的不等式![]() ≤
≤![]() |
|![]() |在[﹣1,1]上恒成立,求实数a的取值范围
|在[﹣1,1]上恒成立,求实数a的取值范围
【答案】(1)偶函数 (2) ![]()
【解析】
(1)函数f(x)是定义域R上的偶函数,用定义法证明即可;(2)由f(x)是R上的偶函数,问题等价于f(x)≤![]() x在[0,1]上恒成立;讨论x=0和x≠0时,求出实数a的取值范围.
x在[0,1]上恒成立;讨论x=0和x≠0时,求出实数a的取值范围.
(1)函数f(x)=x(![]() ﹣
﹣![]() )是定义域R上的偶函数,
)是定义域R上的偶函数,
证明如下:任取x∈R,则f(﹣x)=﹣x(![]() ﹣
﹣![]() )=x(
)=x(![]() ﹣
﹣![]() ),
),
∴f(x)﹣f(﹣x)=x(![]() ﹣
﹣![]() )﹣x(
)﹣x(![]() ﹣
﹣![]() )=x(
)=x(![]() ﹣1)=0,
﹣1)=0,
∴f(﹣x)=f(x),f(x)是偶函数;
(2)由(1)知f(x)是R上的偶函数,∴不等式f(x)≤![]() |x|在[﹣1,1]上恒成立,
|x|在[﹣1,1]上恒成立,
等价于f(x)≤![]() x在[0,1]上恒成立;显然,当x=0时,上述不等式恒成立;
x在[0,1]上恒成立;显然,当x=0时,上述不等式恒成立;
当x≠0时,上述不等式可转化为![]() ﹣
﹣![]() ≤
≤![]() ,∴ax≥
,∴ax≥![]() 在[0,1]上恒成立,
在[0,1]上恒成立,
∴![]() ≤a<1或a>1,
≤a<1或a>1,
∴求实数a的取值范围是[![]() ,1)∪(1,+∞).
,1)∪(1,+∞).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目