题目内容
(2006•蓟县一模)设F1、F2为椭圆的两个焦点,A为椭圆上的点,且
•
=0,cos∠AF1F2=
,则椭圆的离心率为( )
| AF2 |
| F1F2 |
2
| ||
| 3 |
分析:根据向量数量积的性质,由
•
=0得AF2⊥F1F2,Rt△AF1F2中利用三角函数的定义算出|AF1|=
c,利用勾股定理算出|AF2|=
c,进而得到长轴2a=|AF1|+|AF2|=2
c,即可算出该椭圆的离心率.
| AF2 |
| F1F2 |
3
| ||
| 2 |
| ||
| 2 |
| 2 |
解答:解:∵
•
=0,∴
⊥
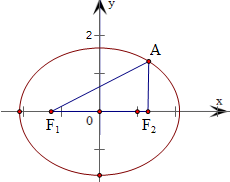
∵Rt△AF1F2中,cos∠AF1F2=
∴
=
,得|AF1|=
|F1F2|=
c
由勾股定理,得|AF2|=
=
c
根据椭圆的定义,得长轴2a=|AF1|+|AF2|=2
c
∴椭圆的离心率e=
=
=
故选:D
| AF2 |
| F1F2 |
| AF2 |
| F1F2 |

∵Rt△AF1F2中,cos∠AF1F2=
2
| ||
| 3 |
∴
| |F 1F2| |
| |AF1| |
2
| ||
| 3 |
3
| ||
| 4 |
3
| ||
| 2 |
由勾股定理,得|AF2|=
| |AF1|2-|F 1F2|2 |
| ||
| 2 |
根据椭圆的定义,得长轴2a=|AF1|+|AF2|=2
| 2 |
∴椭圆的离心率e=
| 2c |
| 2a |
| 2c | ||
2
|
| ||
| 2 |
故选:D
点评:本题给出椭圆中的焦点三角形,在AF2⊥F1F2且cos∠AF1F2=
的情况下求椭圆的离心率.着重考查了向量数量积的性质、直角三角形中三角函数的定义和椭圆的定义与概念等知识,属于基础题.
2
| ||
| 3 |

练习册系列答案
相关题目