题目内容
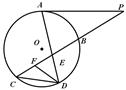
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2 = EF·EC.

(Ⅰ)求证:CE·EB = EF·EP;
(Ⅱ)若CE:BE = 3:2,DE = 3,EF = 2,求PA的长.
【答案】
(I)证得 ∽
∽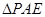
∴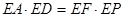
根据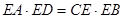 ,得到
,得到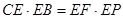 。
。
(II)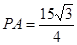 。
。
【解析】
试题分析: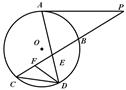
(I)∵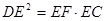 ,
,
∴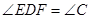 ,
,
又∵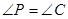 ,∴
,∴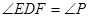 ,
,
∴ ∽
∽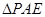
∴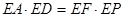
又∵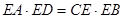 ,
,
∴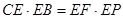 5分
5分
(II) ,
,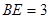 ,
,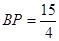
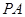 是⊙
是⊙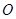 的切线,
的切线,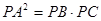 ,
,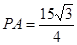 10分
10分
考点:相交弦定理、切割定理、三角形相似。
点评:中档题,作为选考内容,难度不大,主要涉及圆与三角形相似的基础知识。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC. (选修4-1:几何证明选讲)
(选修4-1:几何证明选讲)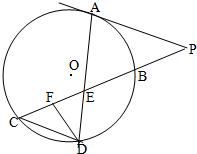 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.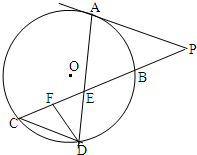 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.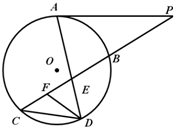 (2013•甘肃三模)选修4-1:几何证明选讲
(2013•甘肃三模)选修4-1:几何证明选讲