题目内容
 22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.(Ⅰ)求证:∠P=∠EDF;
(Ⅱ)求证:CE•EB=EF•EP.
分析:对于(Ⅰ)求证:∠P=∠EDF,因为由已知显然∠C=∠P,故转化为证∠EDF=∠C,则只需根据已知证明△DEF∽△CED,即可得到答案.
(Ⅱ)求证:CE•EB=EF•EP,由(Ⅰ)求得的∠P=∠EDF,和对顶角∠DEF=∠PEA,易得到△DEF∽△PEA.根据相似三角形边的比例关系和圆内两弦相交的比例关系,综合起来即可得到答案.
(Ⅱ)求证:CE•EB=EF•EP,由(Ⅰ)求得的∠P=∠EDF,和对顶角∠DEF=∠PEA,易得到△DEF∽△PEA.根据相似三角形边的比例关系和圆内两弦相交的比例关系,综合起来即可得到答案.
解答:证明:(1)∵DE2=EF•EC,∴DE:CE=EF:ED.
又∵∠DEF是公共角,
∴△DEF∽△CED.∴∠EDF=∠C.
∵CD∥AP,∴∠C=∠P.
∴∠P=∠EDF.
(2)∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.∴DE:PE=EF:EA.即EF•EP=DE•EA.
∵弦AD、BC相交于点E,∴DE•EA=CE•EB.∴CE•EB=EF•EP.
故得证.
又∵∠DEF是公共角,
∴△DEF∽△CED.∴∠EDF=∠C.
∵CD∥AP,∴∠C=∠P.
∴∠P=∠EDF.
(2)∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.∴DE:PE=EF:EA.即EF•EP=DE•EA.
∵弦AD、BC相交于点E,∴DE•EA=CE•EB.∴CE•EB=EF•EP.
故得证.
点评:此题主要考查相似三角形的性质及圆内比例关系的问题,对于此类简单平面几何的问题一般都是基础类型的题目,同学们只需认真分析已知即可得到答案,

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 (选修4-1:几何证明选讲)
(选修4-1:几何证明选讲)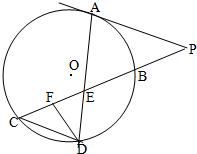 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.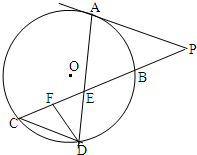 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.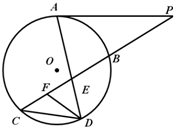 (2013•甘肃三模)选修4-1:几何证明选讲
(2013•甘肃三模)选修4-1:几何证明选讲