题目内容
 (2013•甘肃三模)选修4-1:几何证明选讲
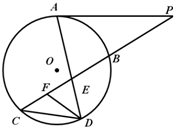
(2013•甘肃三模)选修4-1:几何证明选讲如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2=EF•EC.
(1)求证:CE•EB=EF•EP;
(2)若CE:BE=3:2,DE=3,EF=2,求PA的长.
分析:(I)由已知可得△DEF∽△CED,得到∠EDF=∠C.由平行线的性质可得∠P=∠C,于是得到∠EDF=∠P,再利用对顶角的性质即可证明△EDF∽△EPA.于是得到EA•ED=EF•EP.利用相交弦定理可得EA•ED=CE•EB,进而证明结论;
(II)利用(I)的结论可得BP=
,再利用切割线定理可得PA2=PB•PC,即可得出PA.
(II)利用(I)的结论可得BP=
| 15 |
| 4 |
解答:(I)证明:∵DE2=EF•EC,∠DEF公用,
∴△DEF∽△CED,
∴∠EDF=∠C.
又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA
∴△EDF∽△EPA.
∴
=
,∴EA•ED=EF•EP.
又∵EA•ED=CE•EB,
∴CE•EB=EF•EP;
(II)∵DE2=EF•EC,DE=3,EF=2.
∴32=2EC,∴CE=
.
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴
×3=2EP,解得EP=
,
∴BP=EP-EB=
-3=
.
∵PA是⊙O的切线,∴PA2=PB•PC,
∴PA2=
×(
+
),解得PA=
.
∴△DEF∽△CED,
∴∠EDF=∠C.
又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA
∴△EDF∽△EPA.
∴
| EA |
| EF |
| EP |
| ED |
又∵EA•ED=CE•EB,
∴CE•EB=EF•EP;
(II)∵DE2=EF•EC,DE=3,EF=2.
∴32=2EC,∴CE=
| 9 |
| 2 |
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴
| 9 |
| 2 |
| 27 |
| 4 |
∴BP=EP-EB=
| 27 |
| 4 |
| 15 |
| 4 |
∵PA是⊙O的切线,∴PA2=PB•PC,
∴PA2=
| 15 |
| 4 |
| 27 |
| 4 |
| 9 |
| 2 |
15
| ||
| 4 |
点评:熟练掌握相似三角形的判定和性质定理、平行线的性质、对顶角的性质、相交弦定理、切割线定理是解题的关键.

练习册系列答案
相关题目
 (2013•甘肃三模)在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
(2013•甘肃三模)在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= (2013•甘肃三模)执行如图所示的程序框图,输出的S值为( )
(2013•甘肃三模)执行如图所示的程序框图,输出的S值为( )