题目内容
19.已知函数f(x)和g(x)的图象关于原点对称,且f(x)=$\frac{2}{x}$+$\frac{1}{a}$.(1)求函数g(x)的解析式;
(2)解关于x的不等式g(x)>0;
(3)若g($\frac{t-1}{{t}^{2}}$)≥0在t∈(1,+∞)时恒成立,求a的取值范围.
分析 (1)根据关于原点对称的性质,设出点的坐标,求出g(x)的表达式即可;
(2)通过讨论a的范围,解不等式即可;
(3)通过讨论a的范围,问题分离出a,问题转化为函数恒成立问题,通过讨论函数的单调性,从而求出结果.
解答 解:(1)设M(x,y)是函数y=g(x)图象上任意一点,则M(x,y)关于原点的对称点为N(-x,-y).
则由N在函数f(x)=$\frac{2}{x}$+$\frac{1}{a}$的图象上,可得-y=-$\frac{2}{x}$+$\frac{1}{a}$,∴y=$\frac{2}{x}$-$\frac{1}{a}$,
即g(x)的解析式为:g(x)=$\frac{2}{x}$-$\frac{1}{a}$;
(2)由g(x)=$\frac{2}{x}$-$\frac{1}{a}$>0,得:$\frac{2}{x}$>$\frac{1}{a}$,
①a>0时,x>0时,不等式两边都乘以ax得:0<x<2a,
x<0时,不等式两边都乘以ax得:x>2a>0,矛盾,
②a<0时,x>0时,不等式两边都乘以ax得:2a<x<0,
x<0时,不等式两边都乘以ax得:x<2a;
(3)g($\frac{t-1}{{t}^{2}}$)=$\frac{{2t}^{2}}{t-1}$-$\frac{1}{a}$≥0在t∈(1,+∞)时恒成立,
①a>0时,问题转化为a≥${(\frac{t-1}{{2t}^{2}})}_{max}$在t∈(1,+∞)时恒成立,
设h(t)=$\frac{t-1}{{2t}^{2}}$,h′(t)=$\frac{-2t(t-2)}{{4t}^{4}}$,
令h′(x)>0,解得:1<t<2,令h′(x)<0,解得:t>2,
∴函数h(t)在(1,2)递增,在(2,+∞)递减,
∴h(t)最大值=h(t)极大值=h(2)=$\frac{1}{8}$,
∴a≥$\frac{1}{8}$;
②a<0时,由①得:a≤h(t)最小值即可,
而h(1)=0,t→+∞时,h(t)→0,
∴0<h(t)≤$\frac{1}{8}$,
∴a<0,
综上:a≥$\frac{1}{8}$或a<0.
点评 本题考查了关于原点对称的性质,考查了函数恒成立问题,函数的单调性和最值问题,考查导数的应用,是一道中档题.

| A. | 7!种 | B. | 240种 | C. | 480种 | D. | 960种 |
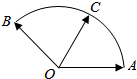 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
| A. | a≤2 | B. | a≥2 | C. | a≤1 | D. | a≥1 |
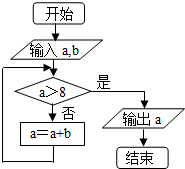
| A. | 7 | B. | 9 | C. | 10 | D. | 13 |
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{2}$ |