题目内容
10．证明：数a=1•2•3…2011+2012•2013…4022能被b=2011+2012整除．分析 利用等差数列的前n项和公式，将数a化为[（1+2011）+（2012+4022）]×2011÷2的形式，化简可得结论．
解答 证明：∵1•2•3…2011+2012•2013…4022
=[（1+2011）+（2012+4022）]×2011÷2
=8046×2011÷2=4023×2011
=（2011+2012）×2011，
故数a=1•2•3…2011+2012•2013…4022能被b=2011+2012整除
点评 本题以整除的判断为载体，考查了等差数列的前n项和公式，难度不大，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1．若直线ax-by+2=0（a＞0，b＞0）被圆x2+y2+4x-4y-1=0所截得的弦长为6，则$\frac{2}{a}+\frac{3}{b}$的最小值为（ ）
| A． | 10 | B． | $4+2\sqrt{6}$ | C． | $5+2\sqrt{6}$ | D． | $4\sqrt{6}$ |
18．方程lgx+x=3的解所在区间为（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
2．已知函数f（x）=$\frac{1}{3}$x3+ax2+b2x+2015（a，b∈R），若从区间[1，3]中任取的一个数a，从区间[0，2]中任取的一个数b，则该函数有两个极值点的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{4}$ | C． | $\frac{7}{8}$ | D． | $\frac{8}{9}$ |
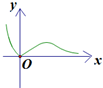
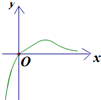
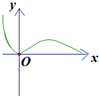
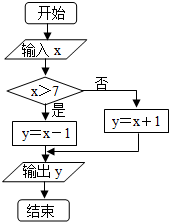x的取值范围为[0，10]，给出如图所示程序框图，输入一个数x．