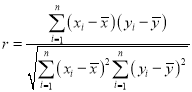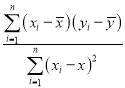题目内容
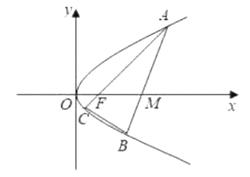
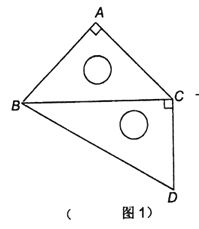
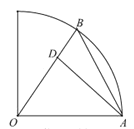
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
【答案】(1)![]() ,
,![]() ;(2)集合地点
;(2)集合地点![]() 离出发点
离出发点![]() 的距离为
的距离为![]() 时,总路程最短,其最短总路程为
时,总路程最短,其最短总路程为![]() .
.
【解析】
(1)先通过正弦定理将AD,BD用![]() 的三角函数表示出来,则
的三角函数表示出来,则![]() ,代入即可得到
,代入即可得到![]() 关于
关于![]() 的函数表达式.(2)令
的函数表达式.(2)令![]() ,对y求导有
,对y求导有![]() 求得y的最小值当且仅当
求得y的最小值当且仅当![]() 时,
时,![]() 有极小值也是最小值为
有极小值也是最小值为![]() ,即可算出AD.
,即可算出AD.
(1)因为在![]() 中,
中,![]() ,
,![]() ,所以由正弦定理可知
,所以由正弦定理可知 ,
,
解得![]() ,
,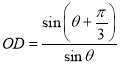 ,且
,且![]() ,
,
故![]()

![]() ,
,![]()
(2)令![]() ,则有
,则有![]() ,令
,令![]() 得
得![]()
记![]() ,
,![]() ,列表得
,列表得
|
|
|
|
|
| 0 |
|
| ↘ | 极小值 | ↗ |
可知,当且仅当![]() 时,
时,![]() 有极小值也是最小值为
有极小值也是最小值为![]() ,
,
当![]() 时,此时总路程
时,此时总路程![]() 有最小值
有最小值![]() .
.
答:当集合点![]() 离出发点
离出发点![]() 的距离为
的距离为![]() 时,总路程最短,其最短总路程为
时,总路程最短,其最短总路程为![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目