题目内容
以椭圆 +
+ =1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于________.
=1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于________.

分析:依据题意先求出椭圆的右焦点坐标、右准线方程,以及圆的半径,利用圆被椭圆的右准线分成弧长为2:1的两段弧,构造直角三角形,利用直角三角形中的边角关系求出离心率.
解答:椭圆的右焦点F(c,0),右准线为 x=
 ,圆的半径为 c,
,圆的半径为 c,圆与右准线的两个交点A,B两点的横坐标为
 ,
,∵圆被椭圆的右准线分成弧长为2:1的两段弧,∴∠AFB=120°
∴△OAB是正三角形,由FA=FB,及∠AFB=120°,构造直角三角形,利用边角关系得
cos60°=
 =
=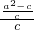 ,
,∴
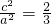 ,
,∴
 =
= ,
,故答案为:
 .
.点评:本题考查椭圆的标准方程和简单性质,利用直角三角形中的边角关系求出离心率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆,过点
=1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆,过点 作圆的两切线互相垂直,则离心率e=( )
作圆的两切线互相垂直,则离心率e=( )


 +
+ =1(a>b>0)的两个焦点,O为坐标原点,点P(-1,
=1(a>b>0)的两个焦点,O为坐标原点,点P(-1, )在椭圆上,且
)在椭圆上,且 •
• =0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B
=0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B •
•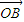 =λ,且满足
=λ,且满足 ≤λ≤
≤λ≤ 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.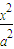 +
+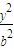 =1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于 .
=1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于 .