题目内容
在平面直角坐标系中,椭圆 =1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆,过点
=1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆,过点 作圆的两切线互相垂直,则离心率e=( )
作圆的两切线互相垂直,则离心率e=( )A.

B.2
C.

D.

【答案】分析:先根据题意画出图形,如图,由切线PA、PB互相垂直,得出△OAP是等腰直角三角形,从而根据直角三角形的边的关系建立a,c之间的关系式,最后解得离心率即可.
解答: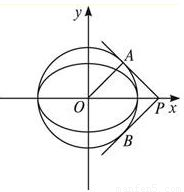 解:法一:如图,切线PA、PB互相垂直,
解:法一:如图,切线PA、PB互相垂直,
又半径OA垂直于PA,
所以△OAP是等腰直角三角形,
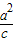 =
=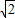 a.
a.
解得e=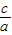 =
=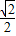 .
.
则离心率e=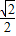 ;
;
法二:关键椭圆的离心率小于1,
分析选项,只有A中的小于1,
故选A.
点评:本小题主要考圆与椭圆的综合、椭圆的几何性质等基础知识,解答的关键是运算求解能力,注意点是数形结合思想.属于基础题.
解答:
 解:法一:如图,切线PA、PB互相垂直,
解:法一:如图,切线PA、PB互相垂直,又半径OA垂直于PA,
所以△OAP是等腰直角三角形,
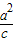 =
=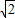 a.
a.解得e=
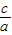 =
=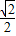 .
.则离心率e=
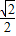 ;
;法二:关键椭圆的离心率小于1,
分析选项,只有A中的小于1,
故选A.
点评:本小题主要考圆与椭圆的综合、椭圆的几何性质等基础知识,解答的关键是运算求解能力,注意点是数形结合思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目