题目内容
已知数列 的通项公式
的通项公式 ,前n项和为
,前n项和为 ,若
,若 ,则
,则 的最大值是( )
的最大值是( )
| A.5 | B.10 | C.15 | D.20 |
B
解析试题分析:由an=-n2+12n-32=0,得n=4或n=8,即a4=a8=0,又函数f(n)=-n2+12n-32的图象开口向下,所以数列前3项为负,当n>8时,数列中的项均为负数,在m<n的前提下,Sn-Sm的最大值是S7-S4=a5+a6+a7=-52+12×5-32-62+12×6-72+12×7-32=10.故选D.
考点:本题考查了数列的函数特性
点评:解答的关键是分清在m<n的前提下,什么情况下Sn最大,什么情况下Sn最小,题目同时考查了数学转化思想.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
数列 满足:
满足: ,
,  ( )
( )
A. | B. | C.5 | D.6 |
数列 则
则 是该数列的( )
是该数列的( )
| A.第6项 | B.第7项 | C.第8项 | D.第9项 |
若1既是 与
与 的等比中项,又是
的等比中项,又是 与
与 的等差中项,则
的等差中项,则 的值是 ( )
的值是 ( )
A.1或 | B.1或 | C.1或 | D.1或 |
若数列 的前n项的和
的前n项的和 ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )
A. | B. |
C. | D. |
下面是关于公差 的等差数列
的等差数列 的四个命题
的四个命题



其中的真命题为
A. | B. | C. | D. |
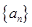 的各项均为正数,前
的各项均为正数,前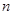 项和为
项和为 ,对于任意的
,对于任意的 ,
,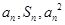 成等差数列,设数列
成等差数列,设数列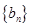 的前
的前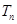 ,且
,且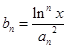 ,则对任意的实数
,则对任意的实数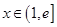 (
(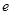 是自然对数的底)和任意正整数
是自然对数的底)和任意正整数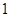
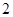
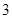
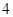
 中,如果存在常数
中,如果存在常数 ,使得
,使得 对于任意正整数
对于任意正整数 均成立,那么 就称数列
均成立,那么 就称数列 叫做数列
叫做数列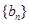 满足
满足 ,若
,若 ,
, ,当数列
,当数列 时,则数列
时,则数列  项的和
项的和 等于( )
等于( )



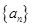 满足
满足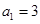 ,
,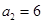 ,且
,且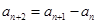 ,则
,则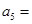 .
.