题目内容
数列 满足:
满足: ,
,  ( )
( )
A. | B. | C.5 | D.6 |
A
解析试题分析:因为 , 则
, 则 .所以
.所以 .即
.即 .故选A.本小题是考差数列的知识,由于通项公式不能直接求出来.是通过累积的形式表达的.这也是本小题的难点.
.故选A.本小题是考差数列的知识,由于通项公式不能直接求出来.是通过累积的形式表达的.这也是本小题的难点.
考点:1.数列的通项问题.2.累积法的思想.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
数列 :
: 、3、
、3、 、9、的一个通项公式是( )
、9、的一个通项公式是( )
A.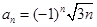 ( (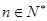 ) ) | B. ( (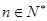 ) ) |
C. ( (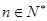 ) ) | D. ( (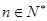 ) ) |
已知数列 满足
满足 ,且
,且 是函数
是函数 的两个零点,则
的两个零点,则 等于( )
等于( )
| A.24 | B.32 | C.48 | D.64 |
已知函数 的图象与直线
的图象与直线 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为 ,则
,则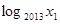 +
+ +…+
+…+ 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
等差数列 中,
中, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
则 的值为( )
的值为( )
| A.18 | B.15 | C.12 | D.20 |
数列 的前
的前 项和为
项和为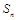 ,若
,若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知数列 的通项公式
的通项公式 ,前n项和为
,前n项和为 ,若
,若 ,则
,则 的最大值是( )
的最大值是( )
| A.5 | B.10 | C.15 | D.20 |
在数列 中,
中, ,则
,则 =( )
=( )
A. |
B. |
C. |
D. |
已知正项数列{an}满足a1=1,(n+2)an+12-(n+1) +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).
A.an= | B.an= |
C.an= | D.an=n |