题目内容
若数列 的前n项的和
的前n项的和 ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )
A. | B. |
C. | D. |
D
解析试题分析:根据前n项和与其通项公式的关系式,an=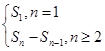
当n≥2时,an=Sn-Sn-1=(3n-2)-(3n-1-2)=2•3n-1.
当n=1时,a1=1,不满足上式;所以an= ,故答案为an=
,故答案为an= ,选D.
,选D.
考点:本题主要考查数列的求和公式,解题时要根据实际情况注意公式的灵活运用,属于中档题
点评:解决该试题的关键是借助公式 an=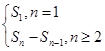 ,将前n项和与其通项公式联系起来得到其通项公式的值。
,将前n项和与其通项公式联系起来得到其通项公式的值。

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
数列 的前
的前 项和为
项和为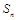 ,若
,若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知数列 的通项公式
的通项公式 ,前n项和为
,前n项和为 ,若
,若 ,则
,则 的最大值是( )
的最大值是( )
| A.5 | B.10 | C.15 | D.20 |
数列{ }中,
}中, ,则{
,则{ }的通项为( )
}的通项为( )
A. -1 -1 | B. | C. +1 +1 | D.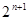 |
已知定义在 上的函数
上的函数 满足
满足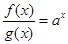 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于
| A.4 | B.5 | C.6 | D.7 |
 中,
中, ,
, ,则
,则 满足
满足 ,
, ,则
,则 的值为_______.
的值为_______. 是等差数列,首项
是等差数列,首项 ,则使前n项和
,则使前n项和 成立的最大自然数n是_______.
成立的最大自然数n是_______.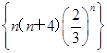 中的最大项是第k项,则k=________.
中的最大项是第k项,则k=________.