题目内容
如图，四棱锥P－ABCD的底面为菱形，且∠ABC－120°，PA⊥底面ABCD，AB＝1，PA＝
，E为PC的中点．
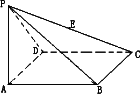
(1)求直线DE与平面PAC所成角的大小；
(2)求二面角E―AD―C的平面角的正切值；
(3)在线段PC上是否存在一点M，使PC⊥平面MBD成立？如果存在，求出MC的长；如果不存在，请说明理由．
答案：
解析：
解析：
|
解：(1)如图，连
又由底面 连 由 又由菱形性质可得，在 所以在 (2)由 过 由(1)可知 (3)设
又 所以 |
，则由
，得平面
．
为菱形，可得
，所以
．
，则
在平面
上的射影，所以
即为
中点可得
．
中，
，所以
．
中，
，所以
;
，
．
作
，连
，则由三垂线定理可得
，所以
即为二面角
的平面角．
，又在
中，
，所以
，所以
;
，过
，则由
．
，所以
．
，而
，可得
，故线段
上存在一点
，使
成立，
．
练习册系列答案
阅读快车系列答案
相关题目
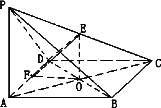
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，CE∥AB．
如图，四棱锥P-ABCD的底面ABCD是正方形，AC∩BD=O，PA⊥底面ABCD，OE⊥PC于E．
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E，F分别是AB和PC的中点．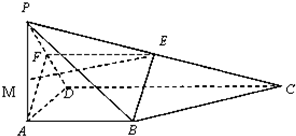
如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=