题目内容
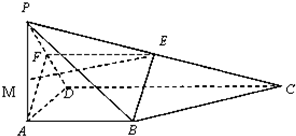 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=| 1 | 2 |
(1)证明:EF∥平面PAB;
(2)证明:PD⊥平面ABEF;
(3)求直线ME与平面ABEF所成角的正弦值.
分析:(1)证明EF∥平面PAB,只需证明AB∥EF,利用三角形中位线的性质及AB∥CD可得;
(2)先证明EF⊥平面PAD,可得EF⊥PD,再证明PD⊥AF,即可证明PD⊥平面ABEF;
(3)求出M到平面ABEF的距离,ME的长,即可求直线ME与平面ABEF所成角的正弦值.
(2)先证明EF⊥平面PAD,可得EF⊥PD,再证明PD⊥AF,即可证明PD⊥平面ABEF;
(3)求出M到平面ABEF的距离,ME的长,即可求直线ME与平面ABEF所成角的正弦值.
解答:(1)证明:∵E、F分别是PC、PD的中点,∴EF∥CD,
∵AB∥CD,
∴AB∥EF,
∵EF?平面PAB,AB?平面PAB,
∴EF∥平面PAB;
(2)证明:∵PA⊥底面ABCD,AB?底面ABCD,
∴PA⊥AB,
∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,
∵AB∥EF,
∴EF⊥平面PAD,
∴EF⊥PD,
∵PA=AD=2,F是PD的中点,
∴PD⊥AF,
∵EF∩AF=F,
∴PD⊥平面ABEF;
(3)解:由(2)知,P到平面ABEF的距离为
,∴M到平面ABEF的距离为
,
又MF=1,EF=2,∴ME=
,
∴直线ME与平面ABEF所成角的正弦值为
=
.
∵AB∥CD,
∴AB∥EF,
∵EF?平面PAB,AB?平面PAB,
∴EF∥平面PAB;
(2)证明:∵PA⊥底面ABCD,AB?底面ABCD,
∴PA⊥AB,
∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,
∵AB∥EF,
∴EF⊥平面PAD,
∴EF⊥PD,
∵PA=AD=2,F是PD的中点,
∴PD⊥AF,
∵EF∩AF=F,
∴PD⊥平面ABEF;
(3)解:由(2)知,P到平面ABEF的距离为
| 2 |
| ||
| 2 |
又MF=1,EF=2,∴ME=
| 5 |
∴直线ME与平面ABEF所成角的正弦值为
| ||||
|
| ||
| 10 |
点评:本题考查线面平行,考查线面垂直,考查线面角,考查学生分析解决问题的能力,考查学生的计算能力,正确运用线面平行,线面垂直的判定定理是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=