题目内容
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.(Ⅰ)求证:CE⊥平面PAD;
(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求点D到平面PCE的距离.
分析:(I)由已知证PA⊥CE,CE⊥AD,由直线与平面垂直的判定定理可得;
(II)由(I)可知CE⊥AD,计算S△CED,S△CEP,利用等体积,即可求得点D到平面PCE的距离.
(II)由(I)可知CE⊥AD,计算S△CED,S△CEP,利用等体积,即可求得点D到平面PCE的距离.
解答: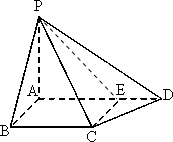 (I)证明:因为PA⊥平面ABCD,CE?平面ABCD,所以PA⊥CE,
(I)证明:因为PA⊥平面ABCD,CE?平面ABCD,所以PA⊥CE,
因为AB⊥AD,CE∥AB,所以CE⊥AD
又PA∩AD=A,所以CE⊥平面PAD
(II)连接PE,由(I)可知CE⊥AD,
∵PA⊥CE,AD∩PA=A,∴CE⊥平面PAD
∵PE?平面PAD,∴CE⊥PE
在Rt△ECD中,DE=CDcos45°=1,CE=CDsin45°=1,∴S△CED=
CE•DE=
在Rt△ECP中,PE=
,CE=1,∴S△CEP=
CE•PE=
设点D到平面PCE的距离为h,利用等体积可得:
×
×1=
×
h
∴h=
.
 (I)证明:因为PA⊥平面ABCD,CE?平面ABCD,所以PA⊥CE,
(I)证明:因为PA⊥平面ABCD,CE?平面ABCD,所以PA⊥CE,因为AB⊥AD,CE∥AB,所以CE⊥AD
又PA∩AD=A,所以CE⊥平面PAD
(II)连接PE,由(I)可知CE⊥AD,
∵PA⊥CE,AD∩PA=A,∴CE⊥平面PAD
∵PE?平面PAD,∴CE⊥PE
在Rt△ECD中,DE=CDcos45°=1,CE=CDsin45°=1,∴S△CED=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ECP中,PE=
| 5 |
| 1 |
| 2 |
| ||
| 2 |
设点D到平面PCE的距离为h,利用等体积可得:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
∴h=
| ||
| 5 |
点评:本题主要考查直线与直线、直线与平面的位置关系,几何体的体积等基础知识,考查数形结合思想,化归与转化的思想.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=