题目内容
已知双曲线
-
=1(a>0)的渐近线为x±y=0,则双曲线的焦距为( )
| ||
|
| y | 2 |
分析:根据双曲线渐近线方程的公式,可得直线y=±
即y=±x,可得a=b=1,再由双曲线基本量的平方关系得c=
=
,由此即可求得该双曲线的焦距.
| x |
| a |
| a2+b 2 |
| 2 |
解答:解:∵双曲线的方程为
-
=1(a>0)
∴双曲线的渐近线方程为y=±
,
结合题意,得y=±
即y=±x,可得a=1(舍负)
∴双曲线的方程为x2-y2=1,得a=b=1
由此可得c=
=
,所以双曲线的焦距2c=2
故选:C
| ||
|
| y | 2 |
∴双曲线的渐近线方程为y=±
| x |
| a |
结合题意,得y=±
| x |
| a |
∴双曲线的方程为x2-y2=1,得a=b=1
由此可得c=
| a2+b 2 |
| 2 |
| 2 |
故选:C
点评:本题给出含有字母参数的双曲线方程,在已知渐近线的情况下求它焦距,着重考查了双曲线的标准方程和简单几何性质等知识点,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知双曲线x2-y2=a2(a>0)的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,∠PAB=α,∠PBA=β,∠APB=γ,则( )
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |
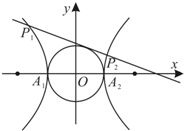 已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).
已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).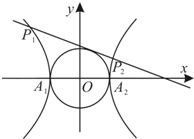 已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).
已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).