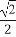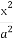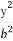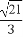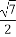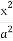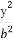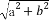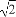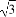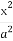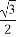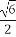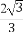题目内容

设P为椭圆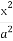+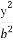=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为　　　　　.

 

[a-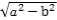,a+]

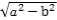【解析】设F2为椭圆的另一焦点,连接PF2,则由椭圆的定义得|PF1|+|PF2|=2a,且c2=a2-b2(c>0).因为||PF1|-|PF2||≤2c.所以-2c≤|PF1|-|PF2|≤2c,所以2a-2c≤2|PF1|≤2a+2c,即a-c≤|PF1|≤a+c,所以|PF1|的最大值为a+c,即a+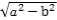,最小值为a-c,即a-.

 

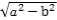练习册系列答案
相关题目

在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为　　　　　　.

 

已知双曲线-=1(a>0,b>0)的一条渐近线方程为y=x,则双曲线的离心率为(　　)

(A) (B) (C) (D)

 

在同一坐标系下,直线ax+by=ab和圆(x-a)2+(y-b)2=r2(ab≠0,r>0)的图象可能是(　　)

 

 

给定椭圆C:+=1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(,0),其短轴上的一个端点到F的距离为.

(1)求椭圆C的方程和其“准圆”的方程.

(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.

①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;

②求证:|MN|为定值.

 

设M(x0,y0)为抛物线C:y2=8x上一点,F为抛物线C的焦点,若以F为圆心,|FM|为半径的圆和抛物线C的准线相交,则x0的取值范围是(　　)

(A)(2,+∞) (B)(4,+∞)

(C)(0,2) (D)(0,4)

 

与直线l:x+y-2=0和曲线x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是　　　　.

 

已知双曲线-y2=1(a>1)的一条准线为x=,则该双曲线的离心率为(　　)

(A) (B) (C) (D)

 

某人站在60米高的楼顶A处测量不可到达的电视塔的高度,测得塔顶C的仰角为30°,塔底B的俯角为15°,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高为　　米.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网