题目内容
8.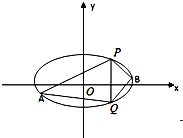 已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点.
已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点.(1)求椭圆C的方程;
(2)点P(2,3),Q(2,-3),在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为$\frac{1}{2}$,求四边形APBQ面积的最大值;
②当A,B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
分析 (1)由题意和双曲线可得b值,进而由离心率和系数的关系可a值,可得椭圆C的方程;
(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=$\frac{1}{2}$x+t,代入$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$消y并整理可得x的二次方程,由韦达定理可得面积S的表达式,由二次函数的最值可得;②设直线PA的斜率为k,则直线PB的斜率为-k,分别联立直线和椭圆的方程由韦达定理可得x1+2=$\frac{8(2k-3)k}{3+4{k}^{2}}$,x2+2=$\frac{8k(2k+3)}{3+4{k}^{2}}$,可得x1+x2=$\frac{16{k}^{2}-12}{3+4{k}^{2}}$,x1-x2=$\frac{-48k}{3+4{k}^{2}}$,代入斜率公式计算可得定值.
解答 解:(1)由题意设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
又可得双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点为(0,±2$\sqrt{3}$),
∴b=2$\sqrt{3}$,又离心率e=$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解得a=4,
∴椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=$\frac{1}{2}$x+t,
代入$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$消y并整理可得x2+tx+t2-12=0,
由△=t2-4(t2-12)>0可解得-4<t<4,
由韦达定理可得x1+x2=-t,x1x2=t2-12,
四边形APBQ的面积S=$\frac{1}{2}$×6×|x1-x2|=3$\sqrt{48-3{t}^{2}}$,
由二次函数可知当t=0时,S取最大值12$\sqrt{3}$
②当∠APQ=∠BPQ时,直线PA和PB的斜率之和为0,
设直线PA的斜率为k,则直线PB的斜率为-k,
∴直线PA的方程为y-3=k(x-2),
联立$\left\{\begin{array}{l}{y-3=k(x-2)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$消去y并整理可得(3+4k2)x2+8(3-2k)kx+4(3-2k)2-48=0
由韦达定理可得x1+2=$\frac{8(2k-3)k}{3+4{k}^{2}}$,
理可得直线PB:y-3=-k(x-2),可得x2+2=$\frac{-8k(-2k-3)}{3+4{k}^{2}}$=$\frac{8k(2k+3)}{3+4{k}^{2}}$,
∴x1+x2=$\frac{16{k}^{2}-12}{3+4{k}^{2}}$,x1-x2=$\frac{-48k}{3+4{k}^{2}}$,
kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}-2)+3-k({x}_{2}-2)-3}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}+{x}_{2})-4k}{{x}_{1}-{x}_{2}}$=$\frac{1}{2}$,
∴直线AB的斜率为定值$\frac{1}{2}$
点评 本题考查直线与圆锥曲线的位置关系,涉及圆锥曲线的取值范围和最值,属难题.

 阅读快车系列答案
阅读快车系列答案 如图,AB是圆O的直径,PA直圆O所在的平面,C是圆O上的点.
如图,AB是圆O的直径,PA直圆O所在的平面,C是圆O上的点.
 如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.