题目内容
过圆x2+y2=1上一点作切线与x轴,y轴的正半轴交于A、B两点,则|AB|的最小值为
- A.

- B.

- C.2
- D.3
C
分析:用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得: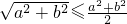 ,令t=
,令t= ,可得t的最小值为 2,进而得到答案.
,可得t的最小值为 2,进而得到答案.
解答:设切线方程为 (a>0,b>0),即 bx+ay-ab=0,
(a>0,b>0),即 bx+ay-ab=0,
由圆心到直线的距离等于半径得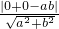 =1,
=1,
所以ab=
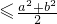 ,令t=
,令t= ,
,
则有t2-2t≥0,t≥2,故t的最小值为 2.
由题意知 t=|AB|,
故选C.
点评:本题考查点到直线的距离公式和基本不等式的应用,体现了换元的思想(在换元时应该注意等价换元).
分析:用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得:
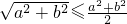 ,令t=
,令t= ,可得t的最小值为 2,进而得到答案.
,可得t的最小值为 2,进而得到答案.解答:设切线方程为
 (a>0,b>0),即 bx+ay-ab=0,
(a>0,b>0),即 bx+ay-ab=0,由圆心到直线的距离等于半径得
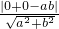 =1,
=1,所以ab=

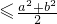 ,令t=
,令t= ,
,则有t2-2t≥0,t≥2,故t的最小值为 2.
由题意知 t=|AB|,
故选C.
点评:本题考查点到直线的距离公式和基本不等式的应用,体现了换元的思想(在换元时应该注意等价换元).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过圆x2+y2=1上一点作切线与x轴,y轴的正半轴交于A、B两点,则|AB|的最小值为( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
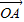 +2
+2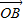 |的最小值是 .
|的最小值是 .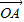 +2
+2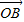 |的最小值是 .
|的最小值是 .