题目内容
过圆x2+y2=1上一点P作圆的切线与x轴和y轴分别交于A,B两点,O是坐标原点,则|
+2
|的最小值是
| OA |
| OB |
3
3
.分析:设∠OBP=α,由O<α<
,∠OAP=
-α,知|
+2
|=|(
,
)|然后利用向量的模以及基本不等式求出表达式的最小值即可.
| π |
| 2 |
| π |
| 2 |
| OA |
| OB |
| 1 |
| cosα |
| 2 |
| sinα |
解答:解:设∠OAP=α,
∵O<α<
,∠OBP=
-α,
=(
,0),2
=(0,
),
∴|
+2
|=|(
,
)|=
=
=
=
≥
=3,当且仅当tan2α=
时,表达式取得最小值.
故答案为:3.
∵O<α<
| π |
| 2 |
| π |
| 2 |
| OA |
| 1 |
| cosα |
| OB |
| 2 |
| sinα |
∴|
| OA |
| OB |
| 1 |
| cosα |
| 2 |
| sinα |
(
|
|
=
|
=
tan2α+
|
≥
| 9 |
| 4 |
| tan2α |
故答案为:3.
点评:本题考查直线和圆的方程的应用,是基础题.解题时要认真审题,仔细解答,注意合理地运用均值不等式进行解题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
过圆x2+y2=1上一点作切线与x轴,y轴的正半轴交于A、B两点,则|AB|的最小值为( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
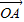 +2
+2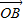 |的最小值是 .
|的最小值是 .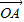 +2
+2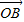 |的最小值是 .
|的最小值是 .