题目内容
已知函数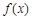 的定义域为
的定义域为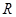 ,若存在常数
,若存在常数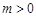 ,对任意
,对任意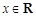 ,有
,有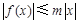 ,则称
,则称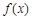 为
为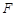 函数.给出下列函数:
函数.给出下列函数:
①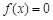 ; ②
; ②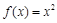 ; ③
; ③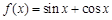 ; ④
; ④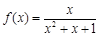 ;
;
⑤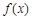 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数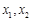 均有
均有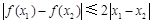 .其中是
.其中是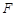 函数的序号是( )
函数的序号是( )
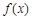 的定义域为
的定义域为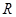 ,若存在常数
,若存在常数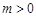 ,对任意
,对任意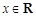 ,有
,有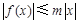 ,则称
,则称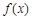 为
为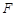 函数.给出下列函数:
函数.给出下列函数:①
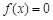 ; ②
; ②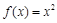 ; ③
; ③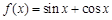 ; ④
; ④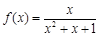 ;
;⑤
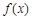 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数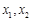 均有
均有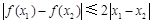 .其中是
.其中是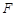 函数的序号是( )
函数的序号是( )| A.①②④ | B.①②⑤ | C.①③④ | D.①④⑤ |
D
试题分析:由函数
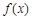 的定义域为
的定义域为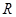 ,若存在常数
,若存在常数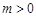 ,对任意
,对任意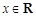 ,有
,有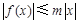 ,则称
,则称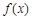 为
为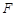 函数,因为
函数,因为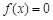 ,所存在
,所存在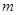 使得
使得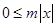 恒成立,所以①正确;若
恒成立,所以①正确;若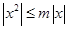 成立,则
成立,则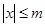 ,显然不存在这样的
,显然不存在这样的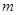 ,所以②不正确;若存在常数
,所以②不正确;若存在常数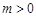 ,对任意
,对任意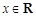 都有
都有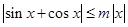 成立,当
成立,当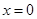 时不成立,所以③不正确;
时不成立,所以③不正确;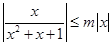 显然存在
显然存在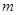 ,所以④正确;若
,所以④正确;若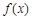 是定义在
是定义在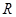 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数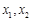 均有
均有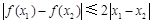 ,令
,令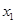 或
或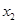 等于零时,即符合要求;综上所述,可知①④⑤正确,故选D.
等于零时,即符合要求;综上所述,可知①④⑤正确,故选D.
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 的函数满足
的函数满足 ,且
,且 ,若
,若 ,则
,则 ( )
( )



 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为 (
( ).
). 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?
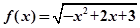 的定义域为 ;
的定义域为 ; ,且
,且 ,则( )
,则( )



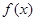 是定义在
是定义在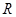 上的函数,且对任意实数
上的函数,且对任意实数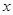 ,都有
,都有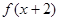 ≤
≤ ,
,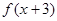 ≥
≥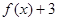 ,且
,且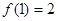 ,
,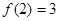 ,则
,则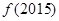 的值是
的值是 和
和 ,定义运算“
,定义运算“ ”,
”, ,则函数
,则函数 ,
, ,若函数
,若函数 的图像与
的图像与 轴有三个交点,则实数
轴有三个交点,则实数 的取值范围
的取值范围