题目内容
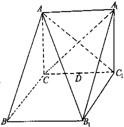 如图所示,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB=2BC,
如图所示,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB=2BC,AC=AA1=
| 3 |
(1)证明:A1C⊥平面AB1C1;
(2)若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?
若存在,请确定点E的位置;若不存在,请说明理由.
分析:(1)根据三边满足勾股定理则△ABC为直角三角形,从而BC⊥AC,又AA1⊥平面ABC,则AA1⊥BC,BC⊥CC1,从而BC⊥面ACC1A1,则BC⊥A1C,则B1C1⊥A1C,因AC=AA1则侧面ACC1A1为正方形,从而AC1⊥A1C,又B1C1∩AC1=C1,根据线面垂直的判定定理可知A1 C⊥面AB1C1;
(2)存在点E,且E为AB的中点,取BB1的中点F,连接DF,则DF∥B1C1,因AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,从而面DEF∥面AB1C1,而DE?面DEF,根据线面平行的判定定理可知DE∥面AB1C1.
(2)存在点E,且E为AB的中点,取BB1的中点F,连接DF,则DF∥B1C1,因AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,从而面DEF∥面AB1C1,而DE?面DEF,根据线面平行的判定定理可知DE∥面AB1C1.
解答:证明:(1)∵AB=2BC,AC=
BC,
∴△ABC为直角三角形,且∠ACB=
.
从而BC⊥AC.又AA1⊥平面ABC,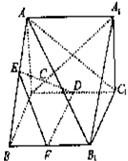
∴AA1⊥BC,∴BC⊥CC1(2分)
从而BC⊥面ACC1A1,∴BC⊥A1C,
则B1C1⊥A1C(4分)∵AC=AA1∴侧面ACC1A1为正方形,∴AC1⊥A1C.
又B1C1∩AC1=C1,∴A1 C⊥面AB1C1(6分)
(2)存在点E,且E为AB的中点((8分))
下面给出证明:
取BB1的中点F,连接DF,则DF∥B1C1.
∵AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,∴面DEF∥面AB1C1.(10分)
而DE?面DEF,∴DE∥面AB1C1(12分)
| 3 |
∴△ABC为直角三角形,且∠ACB=
| π |
| 2 |
从而BC⊥AC.又AA1⊥平面ABC,

∴AA1⊥BC,∴BC⊥CC1(2分)
从而BC⊥面ACC1A1,∴BC⊥A1C,
则B1C1⊥A1C(4分)∵AC=AA1∴侧面ACC1A1为正方形,∴AC1⊥A1C.
又B1C1∩AC1=C1,∴A1 C⊥面AB1C1(6分)
(2)存在点E,且E为AB的中点((8分))
下面给出证明:
取BB1的中点F,连接DF,则DF∥B1C1.
∵AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,∴面DEF∥面AB1C1.(10分)
而DE?面DEF,∴DE∥面AB1C1(12分)
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,同时考查了化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,属于中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
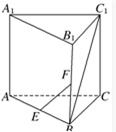 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心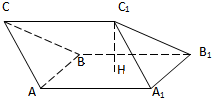 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心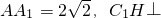 平面AA1B1B且
平面AA1B1B且 .
.
