题目内容
 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心AA1=2| 2 |
| 5 |
(1)求异面直线AC与A1B1所成角的余弦值;
(2)求二面角A-A1C1-B1的正弦值.
分析:(1)通过建立空间直角坐标系,利用异面直线的方向向量的夹角即可得出;
(2)先求出两个平面的法向量的夹角即可得出二面角的余弦值.
(2)先求出两个平面的法向量的夹角即可得出二面角的余弦值.
解答:解:如图所示,建立空间直角坐标系,点B为坐标原点.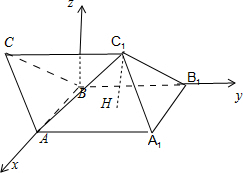
依题意得A(2
,0,0),B(0,0,0),C(
,-
,
),A1(2
,2
,0),
B1(0,2
,0),C1(
,
,
).
(1)易得
=(-
,-
,
),
=(-2
,0,0)
于是cos<
,
>=
=
=
.
∴异面直线AC与A1B1所成角的余弦值为
.
(2)易知
=(0,2
,0),
=(-
,-
,
).
设平面AA1C1的法向量
=(x,y,z),则
,即
,
不妨令x=
,则z=
,可得
=(
,0,
).
同样可设面A1B1C1的法向量
=(x1,y1,z1),得
=(0,
,
).
于是cos<
,
>=
=
=
,∴sin<
,
>=
.
∴二面角A-A1C-B1的正弦值为
.

依题意得A(2
| 2 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
B1(0,2
| 2 |
| 2 |
| 2 |
| 5 |
(1)易得
| AC |
| 2 |
| 2 |
| 5 |
| A1B1 |
| 2 |
于是cos<
| AC |
| A1B1 |
| ||||
|
|
| 4 | ||
3×2
|
| ||
| 3 |
∴异面直线AC与A1B1所成角的余弦值为
| ||
| 3 |
(2)易知
| AA1 |
| 2 |
| A1C1 |
| 2 |
| 2 |
| 5 |
设平面AA1C1的法向量
| m |
|
|
不妨令x=
| 5 |
| 2 |
| m |
| 5 |
| 2 |
同样可设面A1B1C1的法向量
| n |
| n |
| 5 |
| 2 |
于是cos<
| m |
| n |
| ||||
|
|
| 2 | ||||
|
| 2 |
| 7 |
| m |
| n |
3
| ||
| 7 |
∴二面角A-A1C-B1的正弦值为
3
| ||
| 7 |
点评:熟练掌握通过建立空间直角坐标系并利用异面直线的方向向量的夹角求异面直线所成的角、两个平面的法向量的夹角求二面角的方法是解题的关键.

练习册系列答案
相关题目
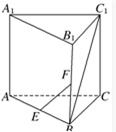 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
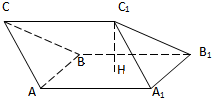 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心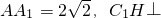 平面AA1B1B且
平面AA1B1B且 .
.
