题目内容
(B题)设函数f(x)=ax3+bx2+cx+d,(a,b,c,d∈R).
(1)若f(x)=(1-2x)3,求3a+2b+c-d的值;
(2)若a=
,b<0,y=f(x)在x=0处取得极值-1,且过点(0,0)可作曲线y=f(x)的三条切线,求b的取值范围.
(1)若f(x)=(1-2x)3,求3a+2b+c-d的值;
(2)若a=
| 1 | 3 |
分析:(1)由于函数f(x)=ax3+bx2+cx+d=(1-2x)3,则导函数也相等,令x=1,则可得3a+2b+c的值,再由二项式定理得到d,即可求3a+2b+c-d的值;
(2)由(1)及a=
,b<0,y=f(x)在x=0处取得极值-1,可得c,d的值,设切点,求切线方程,得到
+b
+1=0,
要求过点(0,0)可作曲线y=f(x)的三条切线,即求g(x)=
x3+bx2+1(b<0)有三个零点,
即是函数的极大值大于0或极小值小于0,即可求得实数b的取值范围.
(2)由(1)及a=
| 1 |
| 3 |
| 2 |
| 3 |
| x | 3 0 |
| x | 2 0 |
要求过点(0,0)可作曲线y=f(x)的三条切线,即求g(x)=
| 2 |
| 3 |
即是函数的极大值大于0或极小值小于0,即可求得实数b的取值范围.
解答:解:(1)∵f(x)=(1-2x)3=ax3+bx2+cx+d,
对此等式两边同时求导数得:3(1-2x)2(-2)=3ax2+2bx+c,
令x=1得:3a+2b+c=-6,又由二项式定理知d=1
故3a+2b+c-d=-6-1=-7…(6分)
(2)∵f′(x)=x2+2bx+c,由题意可得f′(0)=0,f(0)=-1,解得c=0,d=-1
经检验,f(x)在x=0处取得极大值.∴f(x)=
x3+bx-1…(8分)
设切点为(x0,y0),则切线方程为y-y0=f′(x0)(x-x0)
即为y=(
+2bx0)x-
-b
-1…(9分)
因为切线方程为y=(
+2bx0)x-
-b
-1,
把(0,0)代入可得
+b
+1=0,
因为有三条切线,故方程
+b
+1=0有三个不同的实根.…(11分)
设g(x)=
x3+bx2+1(b<0)
∵g′(x)=2x2+2bx,令g′(x)=2x2+2bx=0,可得x=0和x=-b
因为方程有三个根,故极小值小于零,
b3+1<0,所以b<-
…(14分)
对此等式两边同时求导数得:3(1-2x)2(-2)=3ax2+2bx+c,
令x=1得:3a+2b+c=-6,又由二项式定理知d=1
故3a+2b+c-d=-6-1=-7…(6分)
(2)∵f′(x)=x2+2bx+c,由题意可得f′(0)=0,f(0)=-1,解得c=0,d=-1
经检验,f(x)在x=0处取得极大值.∴f(x)=
| 1 |
| 3 |
设切点为(x0,y0),则切线方程为y-y0=f′(x0)(x-x0)
即为y=(
| x | 2 0 |
| 2 |
| 3 |
| x | 3 0 |
| x | 2 0 |
因为切线方程为y=(
| x | 2 0 |
| 2 |
| 3 |
| x | 3 0 |
| x | 2 0 |
把(0,0)代入可得
| 2 |
| 3 |
| x | 3 0 |
| x | 2 0 |
因为有三条切线,故方程
| 2 |
| 3 |
| x | 3 0 |
| x | 2 0 |
设g(x)=
| 2 |
| 3 |
∵g′(x)=2x2+2bx,令g′(x)=2x2+2bx=0,可得x=0和x=-b
| x | (-∞,0) | 0 | (0,-b) | -b | (-b,+∞) |
| g′(x) | + | 0 | 一 | 0 | + |
| g(x) | 增 | 极大值 | 减 | 极小值 | 增 |
| 1 |
| 3 |
| 3 | 3 |
点评:此题主要考查多项式函数的导数,利用导数研究曲线上某点的切线方程,及函数极值等基础知识,考查运算求解能力、推理论证能力及分析与解决问题的能力,难度不大.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 短长度为
短长度为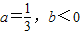 ,y=f(x)在x=0处取得极值-1,且过点(0,0)可作曲线y=f(x)的三条切线,求b的取值范围.
,y=f(x)在x=0处取得极值-1,且过点(0,0)可作曲线y=f(x)的三条切线,求b的取值范围.