题目内容
直线l的参数方程为
(t为参数),圆C:
(α为参数).
(Ⅰ)以原点为极点,x轴的正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(Ⅱ)直线l交圆C于A,B两点,求AB弦长.
|
|
(Ⅰ)以原点为极点,x轴的正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(Ⅱ)直线l交圆C于A,B两点,求AB弦长.
(Ⅰ)把圆C:
(α为参数)利用同角三角函数的基本关系消去参数,
可得圆C的普通方程为x2+y2=4,它的极坐标方程为ρ=2.
(Ⅱ)把直线l的参数方程为
(t为参数),消去参数,化为普通方程为y=-x+2,
圆心到直线l的距离为d=
=
,
由垂径定理得
=
=
,故|AB|=2
.
|
可得圆C的普通方程为x2+y2=4,它的极坐标方程为ρ=2.
(Ⅱ)把直线l的参数方程为
|
圆心到直线l的距离为d=
| 2 | ||
|
| 2 |
由垂径定理得
| |AB| |
| 2 |
| 4-2 |
| 2 |
| 2 |

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
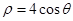 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是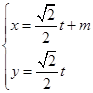 (t是参数).
(t是参数).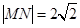 ,求实数m的值.
,求实数m的值.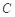 的极坐标方程是
的极坐标方程是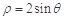 ,直线的参数方程是
,直线的参数方程是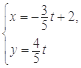 (为参数).
(为参数).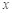 轴的交点是
轴的交点是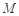 ,
,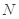 是曲线
是曲线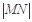 的最大值.
的最大值.