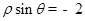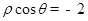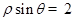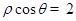题目内容
在极坐标系中,圆ρ=2cosθ的圆心到直线ρcosθ=2的距离是______
将原极坐标方程ρ=2cosθ,化为:
ρ2=2ρcosθ,
化成直角坐标方程为:x2+y2-2x=0,
它表示圆心在(1,0)的圆,
直线ρcosθ=2的直角坐标方程为x=2,
∴所求的距离是:1.
故填:1.
ρ2=2ρcosθ,
化成直角坐标方程为:x2+y2-2x=0,
它表示圆心在(1,0)的圆,
直线ρcosθ=2的直角坐标方程为x=2,
∴所求的距离是:1.
故填:1.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
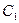 的极坐标方程为
的极坐标方程为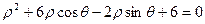 ,曲线
,曲线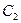 的参数方程为
的参数方程为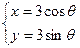 (
(
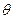 为参
为参 数).
数). 坐标方程化为直角坐标方程;
坐标方程化为直角坐标方程; 线
线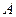 、
、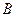 两点,求
两点,求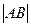 长.
长.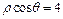 相交于点M,在OM上取一点P,使得
相交于点M,在OM上取一点P,使得 ,求点P的轨迹的极坐标方程.
,求点P的轨迹的极坐标方程.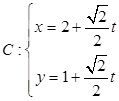 (
(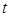 为参数)的普通方程为___________.
为参数)的普通方程为___________.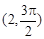 且平行于极轴的直线的极坐标方程是
且平行于极轴的直线的极坐标方程是