题目内容
已知椭圆E的中心在坐标原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; ,
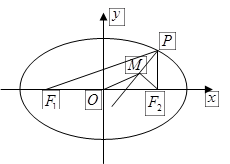
, 是过点
是过点 且相互垂直的两条直线,
且相互垂直的两条直线, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, ,
, 的中点分别为
的中点分别为 ,
, .
.
(1)求椭圆E的标准方程;
(2)求直线 的斜率
的斜率 的取值范围;
的取值范围;
(3)求证直线 与直线
与直线 的斜率乘积为定值.
的斜率乘积为定值.
 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; ,
, 是过点
是过点 且相互垂直的两条直线,
且相互垂直的两条直线, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, 交椭圆E于
交椭圆E于 ,
, 两点,
两点, ,
, 的中点分别为
的中点分别为 ,
, .
.(1)求椭圆E的标准方程;
(2)求直线
 的斜率
的斜率 的取值范围;
的取值范围;(3)求证直线
 与直线
与直线 的斜率乘积为定值.
的斜率乘积为定值.(1)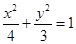 . (2)
. (2)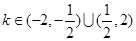 . (3)
. (3)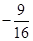
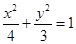 . (2)
. (2)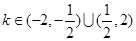 . (3)
. (3)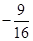
本试题主要是考出了椭圆方程的求解,已知直线与椭圆的位置关系的运用,求解直线的斜率问题,韦达定理的运用,以及判别式的综合运用。
(1)结合椭圆的性质,得到关于a,b,c的关系式,进而得到结论。
(2)设出直线方程,直线与椭圆的方程联立,得到关于未知数的一元二次方程,然后借助于韦达定理和判别式得到k的取值范围。
(3)利用两点式得到直线的斜率,借助于韦达定理求证其积为定值。
(1)设椭圆E的方程为 ,
,
由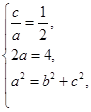 得
得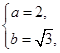 所以所求椭圆E的标准方程为
所以所求椭圆E的标准方程为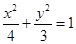 . …… 4分
. …… 4分
(2)由题意知,直线 的斜率存在且不为零,由于
的斜率存在且不为零,由于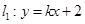 ,则
,则 ,
,
由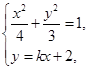 消去
消去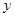 并化简整理,得
并化简整理,得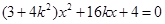 , …… …… 6分
, …… …… 6分
根据题意,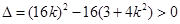 ,解得
,解得 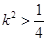 ,同理可得
,同理可得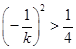 ,即
,即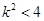 ,
,
∴有 ,解得
,解得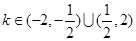 . …… 8分
. …… 8分
(3)设 ,
,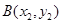 ,
,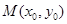 ,那么
,那么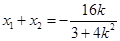 ,
,
则 ,
,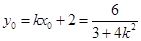 ,即
,即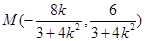 , 10分
, 10分
同理可得 ,即
,即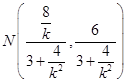 ,
,
∴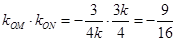 ,即直线
,即直线 与直线
与直线 的斜率乘积为定值
的斜率乘积为定值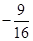
(1)结合椭圆的性质,得到关于a,b,c的关系式,进而得到结论。
(2)设出直线方程,直线与椭圆的方程联立,得到关于未知数的一元二次方程,然后借助于韦达定理和判别式得到k的取值范围。
(3)利用两点式得到直线的斜率,借助于韦达定理求证其积为定值。
(1)设椭圆E的方程为
 ,
,由
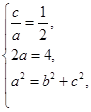 得
得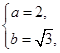 所以所求椭圆E的标准方程为
所以所求椭圆E的标准方程为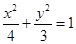 . …… 4分
. …… 4分(2)由题意知,直线
 的斜率存在且不为零,由于
的斜率存在且不为零,由于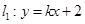 ,则
,则 ,
,由
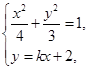 消去
消去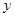 并化简整理,得
并化简整理,得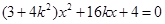 , …… …… 6分
, …… …… 6分根据题意,
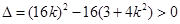 ,解得
,解得 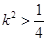 ,同理可得
,同理可得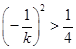 ,即
,即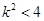 ,
,∴有
 ,解得
,解得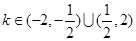 . …… 8分
. …… 8分(3)设
 ,
,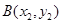 ,
,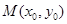 ,那么
,那么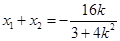 ,
,则
 ,
,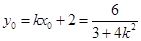 ,即
,即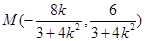 , 10分
, 10分同理可得
 ,即
,即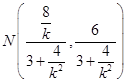 ,
,∴
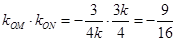 ,即直线
,即直线 与直线
与直线 的斜率乘积为定值
的斜率乘积为定值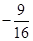

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
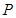 为圆
为圆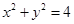 上的动点,且
上的动点,且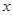 轴上,
轴上,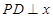 轴,垂足为
轴,垂足为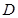 ,线段
,线段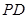 中点
中点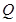 的轨迹为曲线
的轨迹为曲线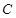 ,过定点
,过定点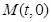
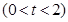 任作一条与
任作一条与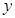 轴不垂直的直线
轴不垂直的直线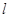 ,它与曲线
,它与曲线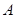 、
、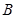 两点。
两点。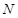 ,使得
,使得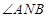 总能被
总能被 ),若
),若 的最小值为1,则椭圆的离心率为 。
的最小值为1,则椭圆的离心率为 。 的离心率
的离心率 右焦点到直线
右焦点到直线 的距离
的距离 ,
, 为坐标原点。
为坐标原点。
 的方程;
的方程; 两点,证明点
两点,证明点 的距离为定值,并求弦
的距离为定值,并求弦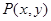 为动点,已知点
为动点,已知点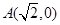 ,
,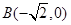 ,直线
,直线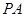 与
与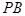 的斜率之积为
的斜率之积为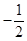 .
. 轨迹
轨迹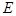 的方程;
的方程;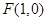 的直线
的直线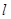 交曲线
交曲线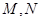 两点,设点
两点,设点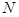 关于
关于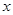 轴的对称点为
轴的对称点为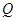 (
(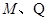 不重合),求证:直线
不重合),求证:直线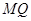 过定点.
过定点. 的离心率为
的离心率为 ,点
,点 ,
,  为
为 上两点,斜率为
上两点,斜率为 的直线与椭圆
的直线与椭圆 交于点
交于点 ,
, (
( 两侧).
两侧).
 面积的最大值;
面积的最大值; ,
, 的斜率为
的斜率为 ,试判断
,试判断 是否为定值.若是,求出这个定值;若不是,说明理由.
是否为定值.若是,求出这个定值;若不是,说明理由. 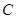 以
以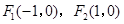 为焦点,且离心率
为焦点,且离心率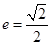 .
. 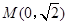 点斜率为
点斜率为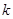 的直线
的直线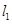 与椭圆
与椭圆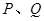 ,求
,求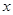 轴正半轴、
轴正半轴、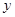 轴正半轴的交点分别为
轴正半轴的交点分别为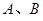 ,是否存在直线
,是否存在直线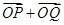 与
与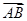 垂直?如果存在,写出
垂直?如果存在,写出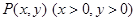 是双曲线
是双曲线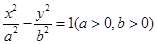 上的动点,
上的动点,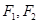 是双曲线的焦点,
是双曲线的焦点,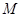 是
是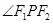 的平分线上一点,且
的平分线上一点,且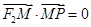 .某同学用以下方法研究
.某同学用以下方法研究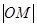 :延长
:延长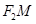 交
交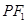 于点
于点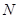 ,可知
,可知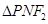 为等腰三角形,且
为等腰三角形,且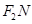 的中点,得
的中点,得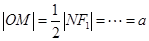 .类似地:点
.类似地:点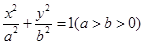 上的动点,
上的动点,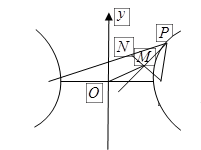
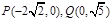 的椭圆标准方程( ).
的椭圆标准方程( ).


