Question

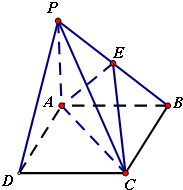（2013•南充三模）如图，在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，PA⊥平面ABCD，E为PB中点，PB=4

2

．
（I）求证：PD∥面ACE．
（Ⅱ）求三棱锥E-ABC的体积．

Answer 1

分析：（I）连接BD，交AC于F，连接EF，证明EF∥PD，利用线面平行的判定定理，可得结论；
（II）取AB中点为G，连接EG，证明EG⊥平面ABCD，即可求三棱锥E-ABC的体积．

解答：（I）证明：连接BD，交AC于F，连接EF．
∵四边形ABCD为正方形   
∴F为BD的中点
∵E为PB的中点，
∴EF∥PD
又∵PD?面 ACE，EF?面ACE，
∴PD∥平面ACE …（5分）
（Ⅱ）解：取AB中点为G，连接EG
∵E为AB的中点
∴EG∥PA
∵PA⊥平面ABCD，
∴EG⊥平面ABCD，
在Rt△PAB中，PB=4

2

，AB=4，则PA=4，EG=2…（10分）
∴V=

1

3

S△ABC•EG=

1

3

×

1

2

×42×2=

16

3

…（12分）

点评：本题考查线面平行，考查三棱锥体积的计算，考查学生分析解决问题的能力，属于中档题．