题目内容
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,直线
,直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,且分别交椭圆于
,且分别交椭圆于![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求得椭圆的焦点坐标,连接![]() ,由垂直平分线的性质可得
,由垂直平分线的性质可得![]() ,运用抛物线的定义,即可得到所求轨迹方程;(2)分类讨论:当
,运用抛物线的定义,即可得到所求轨迹方程;(2)分类讨论:当![]() 或
或![]() 中的一条与
中的一条与![]() 轴垂直而另一条与
轴垂直而另一条与![]() 轴重合时,此时四边形
轴重合时,此时四边形![]() 面积
面积![]() .当直线
.当直线![]() 和
和![]() 的斜率都存在时,不妨设直线
的斜率都存在时,不妨设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .分别与椭圆的方程联立得到根与系数的关系,利用弦长公式可得
.分别与椭圆的方程联立得到根与系数的关系,利用弦长公式可得![]() ,
,![]() .利用四边形
.利用四边形![]() 面积
面积![]() 即可得到关于斜率
即可得到关于斜率![]() 的式子,再利用配方和二次函数的最值求法,即可得出.
的式子,再利用配方和二次函数的最值求法,即可得出.
试题解析:解:(1)∵![]() ,∴点
,∴点![]() 到定直线
到定直线![]() :
:![]() 的距离等于它到定点
的距离等于它到定点![]() 的距离,∴点
的距离,∴点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为准线,
为准线,![]() 为焦点的抛物线.
为焦点的抛物线.
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率存在且不为零时,直线
的斜率存在且不为零时,直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立
,联立 ,得
,得![]() .
.
∴![]() ,
,![]() .
.
![]() .由于直线
.由于直线![]() 的斜率为
的斜率为![]() ,用
,用![]() 代换上式中的
代换上式中的![]() 。可得
。可得![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 的面积
的面积![]() .
.
由于![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取得等号.
时取得等号.
易知,当直线![]() 的斜率不存在或斜率为零时,四边形
的斜率不存在或斜率为零时,四边形![]() 的面积
的面积![]() .
.
综上,四边形![]() 面积的最小值为
面积的最小值为![]() .
.

【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: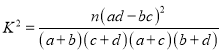 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
