题目内容
【题目】已知函数
（
且
）.
（1）讨论
的单调性；
（2）对任意
，
恒成立，求
的取值范围.
【答案】（1）答案不唯一，具体见解析（2）
【解析】
(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2) 由题意知对任意
，
恒成立，
，又由（1）可知，
在区间
上单调递减，在区间
上单调递增.所以只需：
，设
，对其求导可得函数的单调性，从而可求得实数
的取值范围.
解：（1）由
.令
得
，
当
时，
时，
，单调递减；
时，
，单调递增.
当
时，时，，单调递减；时，
，单调递增.
综上所述，在区间
上单调递减，在区间
上单调递增.
（2）由题意知对任意，
恒成立，，
又由（1）知，在区间上单调递减，在区间上单调递增.所以只需：
，
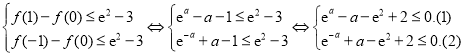设.
∵
，∴
在区间上单调递增；在区间上单调递减.
注意到
，所以，当
不等式（1）成立；当
时不等式（1）不成立.
又
，∴当
不等式（1）也成立，
所以，
时不等式（1）成立.此时，不等式（2）也成立，而当
时，
，由函数的性质知，不等式（2）不成立.
综上所述，不等式组的解为.
又∵
，∴实数的取值范围为.
练习册系列答案
智慧小复习系列答案
相关题目
【题目】从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：
质量指标值分组 | [75，85) | [85，95) | [95，105) | [105，115) | [115，125) |
频数 | 6 | 26 | 38 | 22 | 8 |
（I）在答题卡上作出这些数据的频率分布直方图：
（II）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；
（III）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？
