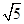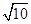题目内容
如图,在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB是等边三角形.
1、求PC与平面ABCD所成角的正弦值;
2、求二面角B—AC—P的余弦值;
求点A到平面PCD的距离.
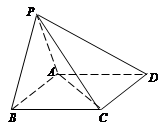
1、求PC与平面ABCD所成角的正弦值;
2、求二面角B—AC—P的余弦值;
求点A到平面PCD的距离.
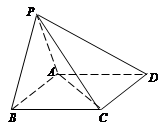
(1) 取AB中点E,则PE⊥AB
∵ 平面PAB⊥平面ABCD
∴ PE⊥平面ABCD
取CD中点F,连结EF
如图,建立空间直角坐标系E—xyz,则P(0,0,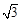 ),C(1, 2,0)
),C(1, 2,0)
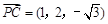
平面ABCD的一个法向量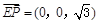
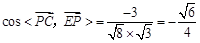

∴ PC与平面ABCD所成角的正弦值为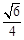
(2) A(– 1,0,0),C(1,2,0),P(0,0,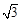 )
)

∴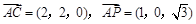
平面APC的一个法向量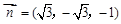
平面ABC的一个法向量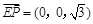
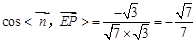
∴ 二面角B—AC—P的余弦值为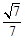
(3) P(0,0,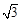 ),C(1,2,0),D(– 1,2,0)
),C(1,2,0),D(– 1,2,0)

∴ 平面PCD的一个法向量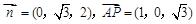
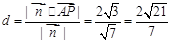
∴ 点A到平面PCD的距离为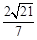
∵ 平面PAB⊥平面ABCD
∴ PE⊥平面ABCD
取CD中点F,连结EF
如图,建立空间直角坐标系E—xyz,则P(0,0,
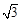 ),C(1, 2,0)
),C(1, 2,0)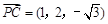
平面ABCD的一个法向量
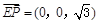
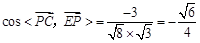

∴ PC与平面ABCD所成角的正弦值为
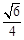
(2) A(– 1,0,0),C(1,2,0),P(0,0,
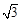 )
)
∴
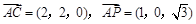
平面APC的一个法向量
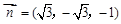
平面ABC的一个法向量
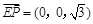
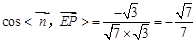
∴ 二面角B—AC—P的余弦值为
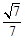
(3) P(0,0,
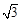 ),C(1,2,0),D(– 1,2,0)
),C(1,2,0),D(– 1,2,0)
∴ 平面PCD的一个法向量
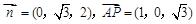
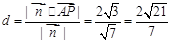
∴ 点A到平面PCD的距离为
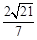
略

练习册系列答案
相关题目
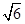 ,M是CC1的中点.
,M是CC1的中点.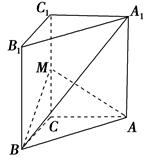
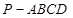 的底面是平行四边形,
的底面是平行四边形,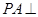 平面
平面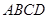 ,
,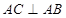 ,
,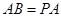 ,
,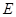 是
是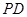 上的点,且
上的点,且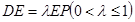 .
. 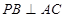 ;
;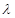 的值,使
的值,使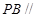 平面
平面 ;
;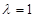 时,求三棱锥
时,求三棱锥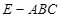 与四棱锥
与四棱锥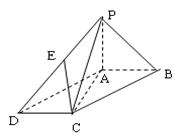
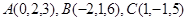 ,则以AB,AC为边的平行四边形的面积____
,则以AB,AC为边的平行四边形的面积____ 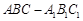 中,△ABC为等边三角形,侧棱
中,△ABC为等边三角形,侧棱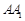 ⊥平面
⊥平面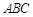 ,
,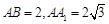 ,D、E分别为
,D、E分别为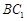 的中点.
的中点.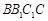 ;
;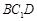 所成角;
所成角;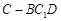 的体积.
的体积.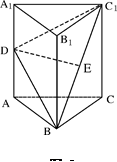
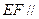 平面
平面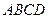 ;
; 平面
平面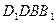 .
.
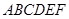 中,
中,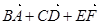
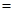 ( )
( )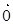
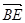
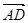
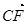
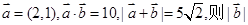 = ( ▲)
= ( ▲)