题目内容
13.函数f(x)=cos2x+sinx-2,x∈($\frac{π}{12}$,$\frac{7π}{6}$]的值域为[-$\frac{7}{4}$,-$\frac{3}{4}$].分析 根据三角函数结合一元二次函数的性质进行求解即可.
解答 解:f(x)=cos2x+sinx-2=1-sin2x+sinx-2,
=-(sinx-$\frac{1}{2}$)2-$\frac{3}{4}$,
∵x∈($\frac{π}{12}$,$\frac{7π}{6}$],
∴sinx∈[sin$\frac{7π}{6}$,sin$\frac{π}{2}$],即sinx∈[$-\frac{1}{2}$,1],
∴当sinx=$\frac{1}{2}$,函数f(x)取得最大值-$\frac{3}{4}$,
当sinx=-$\frac{1}{2}$,函数f(x)取得最小值-$\frac{7}{4}$,
故函数的值域为[-$\frac{7}{4}$,-$\frac{3}{4}$],
故答案为:[-$\frac{7}{4}$,-$\frac{3}{4}$]
点评 本题主要考查三角函数的值域的求解,利用三角函数的单调性以及一元二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
4.某产品的广告支出x(单位:万元)与销售收入y(单位:万元)之间有下表所对应的数据:
(1)画出表中数据的散点图;
(2)求出y对x的回归直线方程;
(3)若广告费为9万元,则销售收入约为多少万元?( $\sum_{i=1}^4{{x_i}{y_i}}=418$,$\sum_{i=1}^4{{x_i}^2}=30$$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
| 销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
(2)求出y对x的回归直线方程;
(3)若广告费为9万元,则销售收入约为多少万元?( $\sum_{i=1}^4{{x_i}{y_i}}=418$,$\sum_{i=1}^4{{x_i}^2}=30$$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}},\hat a=\bar y-\hat b\bar x$)
18.下面三视图的实物图形的名称是( )
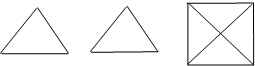

| A. | 四棱锥 | B. | 四棱台 | C. | 三棱柱 | D. | 三棱锥 |
2.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a;
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{a=\widehat{y}-b\overline{x}}\end{array}\right.$.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a;
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{a=\widehat{y}-b\overline{x}}\end{array}\right.$.