题目内容
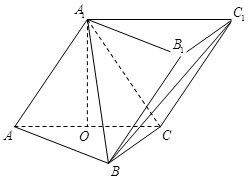
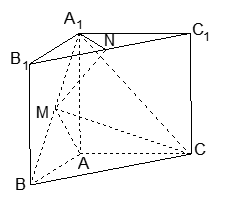
(12分)已知直三棱柱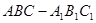 中,
中,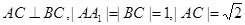 ,点M是
,点M是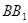 的中点,Q是AB的中点,
的中点,Q是AB的中点,
(1)若P是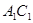 上的一动点,求证:
上的一动点,求证: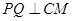 ;
;
(2)求二面角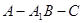 大小的余弦值.
大小的余弦值.
(2)
解析试题分析:(1)取BC的中点E,连接EQ,因为Q为AB的中点,所以EQ//A1C1,因为AC ,此三棱柱为直三棱柱,所以
,此三棱柱为直三棱柱,所以 ,所以
,所以 ,又因为BC=CC1=1,所以四边形BB1C1C为正方形,所以
,又因为BC=CC1=1,所以四边形BB1C1C为正方形,所以 ,所以
,所以 ,所以
,所以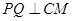 .
.
(2)过C作CN 于N点,过N作作
于N点,过N作作 ,连接FC,
,连接FC,
则 就是二面角
就是二面角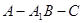 大小的平面角,
大小的平面角,
在 中,
中,

所以二面角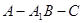 大小的余弦值为
大小的余弦值为 .
.
考点:线面垂直的判定,二面角.
点评:在证明直线与直线垂直时可考虑使用线面垂直的性质定理证明直线垂直另一条直线所在的平面即可.求二面角关键是找出或做出其平面角,常用做平面角的方法就是三垂线定理.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
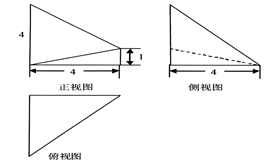
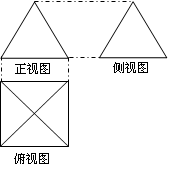
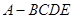 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.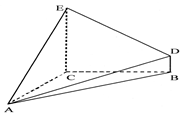
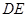 与
与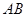 所成角的余弦值;
所成角的余弦值;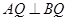 ,并说明理由.
,并说明理由.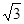 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.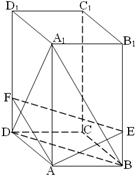
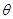 的正切值.
的正切值.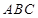
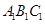 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,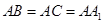
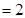 ,点
,点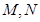 分别为
分别为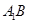 和
和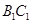 的中点.
的中点.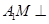 平面
平面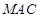 ;
;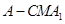 的体积;
的体积;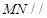 平面
平面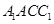 .
.
 中,底面
中,底面 是直角梯形,
是直角梯形,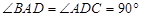 ,
, ,
,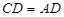 .
.
 是二面角
是二面角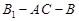 的平面角;
的平面角; 上是否存一点
上是否存一点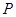 ,使得
,使得 与平面
与平面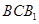 与平面
与平面 都平行?证明你的结论.
都平行?证明你的结论.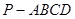 的侧面
的侧面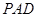 垂直于底面
垂直于底面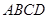 ,
,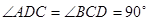
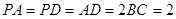 ,
,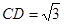 ,
,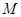 在棱
在棱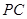 上,
上,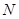 是
是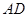 的中点,二面角
的中点,二面角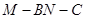 为
为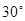 求
求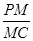 的值;
的值;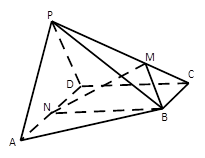
 满足
满足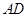 ∥
∥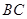 ,
,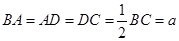 ,
,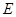 是
是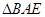 沿着
沿着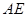 翻折成
翻折成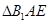 ,使面
,使面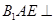 面
面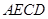 ,
, 为
为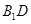 的中点.
的中点. 
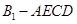 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: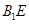 ∥面
∥面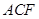 ;
;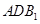 与面
与面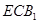 所成二面角的余弦值.
所成二面角的余弦值.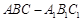 中,侧面
中,侧面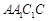
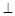 底面
底面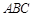 ,
,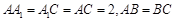 ,且
,且 ,O为
,O为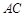 中点.
中点.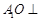 平面
平面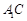 与平面
与平面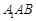 所成角的正弦值
所成角的正弦值