题目内容
(本题满分14分)已知二次函数![]() :
:
(1)若函数在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)问:是否存在常数![]() ,当
,当![]() 时,
时,![]() 的值域为区间
的值域为区间![]() ,且
,且![]()
的长度为![]() 。
。
![]() ,
,
解析:
解:⑴ ∵二次函数![]() 的对称轴是
的对称轴是![]()
∴函数![]() 在区间
在区间![]() 上单调递减
上单调递减
∴要函数![]() 在区间
在区间![]() 上存在零点须满足
上存在零点须满足![]()
即 ![]()
解得 ![]() --------------------------------------4分
--------------------------------------4分
⑵ 当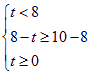 时,即
时,即![]() 时,
时,![]() 的值域为:
的值域为:![]() ,
,
即 ![]()
∴![]()
∴![]() ∴
∴![]()
经检验![]() 不合题意,舍去。---------------------------7分
不合题意,舍去。---------------------------7分
当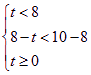 时,即
时,即![]() 时,
时,![]() 的值域为:
的值域为:![]() ,
,
即 ![]()
∴![]()
∴![]()
经检验![]() 不合题意,舍去。-------------------------------------10分
不合题意,舍去。-------------------------------------10分
当![]() 时,
时,![]() 的值域为:
的值域为:![]() ,
,
即 ![]()
∴![]()
∴![]() ∴
∴![]() 或
或![]()
经检验![]() 或
或![]() 满足题意。------------------------------------13分
满足题意。------------------------------------13分
所以存在常数![]() ,当
,当![]() 时,
时,![]() 的值域为区间
的值域为区间![]() ,且
,且![]() 的长度为
的长度为![]() 。
。
------------------14分

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
