题目内容
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为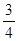 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为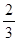 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分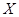 的分布列及数学期望
的分布列及数学期望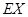 ;
;
(I)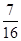 .
.
(II)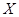 的分布列是
的分布列是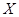
0 1 2 3 4 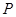
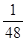
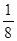
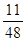
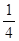
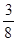
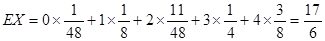 .
.
解析试题分析:(I)此类题的一般解法是,标记事件,计算概率,注意到记:“该射手恰好命中两次”为事件 ,“该射手第一次射击甲靶命中”为事件
,“该射手第一次射击甲靶命中”为事件 ,“该射手第二次射击甲靶命中”为事件
,“该射手第二次射击甲靶命中”为事件 ,“该射手射击乙靶命中”为事件
,“该射手射击乙靶命中”为事件 .可得,
.可得,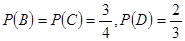 ,
,
进一步利用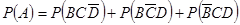
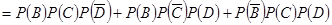
计算即得.
(II)注意到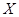 的所有可能取值为0,1,2,3,4.利用独立事件同时发生的概率计算公式可得.细心计算是关键.
的所有可能取值为0,1,2,3,4.利用独立事件同时发生的概率计算公式可得.细心计算是关键.
试题解析:(I)记:“该射手恰好命中两次”为事件 ,“该射手第一次射击甲靶命中”为事件
,“该射手第一次射击甲靶命中”为事件 ,“该射手第二次射击甲靶命中”为事件
,“该射手第二次射击甲靶命中”为事件 ,“该射手射击乙靶命中”为事件
,“该射手射击乙靶命中”为事件 .
.
由题意知,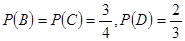 ,
,
所以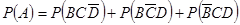
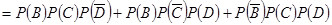
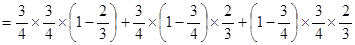
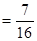 . 6分
. 6分
(II)根据题意, 的所有可能取值为0,1,2,3,4.
的所有可能取值为0,1,2,3,4. ,
,
 .
.
 ,
,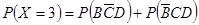
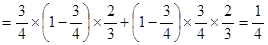 ,
,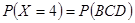
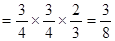 , 11分
, 11分
故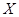 的分布列是
的分布列是
12分
0 1 2 3 4 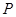
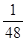
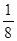
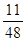
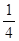
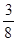
所以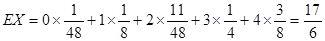 . 14分
. 14分
考点:独立事件同时发生的概率,随机变量的分布列及数学期望.

已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)根据上表,利用最小二乘法,求出
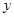 关于
关于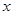 的线性回归方程
的线性回归方程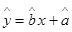 ,
,其中
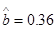
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.(四舍五入到整数)
(12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生
(I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.

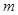 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求
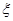 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出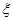 ,求随机变量
,求随机变量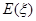 .
.
 的值;
的值;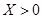 就去打球;若
就去打球;若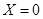 就去唱歌;若
就去唱歌;若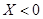 就去下棋.
就去下棋.