题目内容
已知 、
、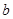 、
、 分别是
分别是 的三个内角
的三个内角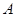 、
、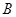 、
、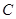 的对边.
的对边.
(1)若 面积
面积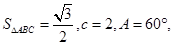 求
求 、
、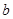 的值;
的值;
(2)若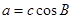 ,且
,且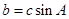 ,试判断
,试判断 的形状.
的形状.
(1) ,
, ,(2)等腰直角三角形.
,(2)等腰直角三角形.
解析试题分析:(1)解三角形问题,一般利用正余弦定理进行边角转化.首先根据面积公式解出b边,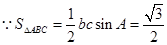
 得
得 ,再由由余弦定理得:
,再由由余弦定理得: ,所以
,所以 ,(2)判断三角形形状,利用边的关系比较直观. 因为
,(2)判断三角形形状,利用边的关系比较直观. 因为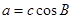 ,所以由余弦定理得:
,所以由余弦定理得: ,所以
,所以 ,在
,在 中,
中, ,所以
,所以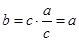 ,所以
,所以 是等腰直角三角形.
是等腰直角三角形.
解:(1)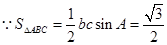 , 2分
, 2分 ,得
,得 3分
3分
由余弦定理得: , 5分
, 5分
所以 6分
6分
(2)由余弦定理得: ,所以
,所以 9分
9分
在 中,
中, ,所以
,所以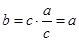 11分
11分
所以 是等腰直角三角形; 12分
是等腰直角三角形; 12分
考点:正余弦定理

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
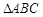 中,内角
中,内角 ,
,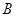 ,
,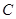 所对的边分别为
所对的边分别为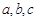 ,已知
,已知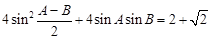
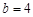 ,
,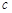 的值.
的值. 中,
中, 分别为角
分别为角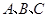 的对边,且满足
的对边,且满足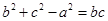 .
.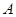 的值;
的值;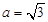 ,求bc最大值.
,求bc最大值.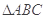 中,角
中,角 、
、 、
、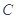 的对边分别为
的对边分别为 、
、 、
、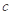 ,
, ,
, .
.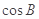 的值;(2) 设函数
的值;(2) 设函数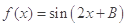 ,求
,求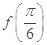 的值.
的值.
 b2.
b2. ,b=1时,求a,c的值;
,b=1时,求a,c的值;
 ,向量
,向量
 .
. ,b+c=3,求b,c的长.
,b+c=3,求b,c的长. 中,A、B、C的对边分别是a、b、c,且A、B、C成等差数列.
中,A、B、C的对边分别是a、b、c,且A、B、C成等差数列. .
.  ,求:a,c的值.
,求:a,c的值.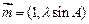 ,
,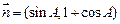 .已知
.已知 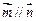 .
.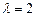 ,求角A的大小;
,求角A的大小;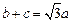 ,求
,求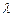 的取值范围。
的取值范围。