Question

18．已知在60°二面角M-α-N内有一点P，P到平面M、平面N的距离均为2，求点P到直线a的距离．

Answer 1

分析 设PA、PB分别为点P到平面M、N的距离，过PA、PB作平面α，分别交M、N于AQ、BQ，根据二面角平面角的定义可知∠AQB是二面角M-a-N的平面角，连PQ，则PQ是P到a的距离，PQ是四边形PAQB的外接圆的直径2R，在△PAB中由余弦定理得 求出AB，最后根据正弦定理可求出PQ，从而求出点P到直线a的距离．

解答 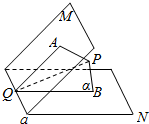解：设PA、PB分别为点P到平面M、N的距离，过PA、PB作平面α，分别交M、N于AQ、BQ． 　　
PA⊥平面M，a?平面M，则PA⊥a，同理，有PB⊥a，
∵PA∩PB=P，∴a⊥面PAQB于Q
又AQ、BQ?平面PAQB，∴AQ⊥a，BQ⊥a．
∴∠AQB是二面角M-a-N的平面角，
∴∠AQB=60°
连PQ，则PQ是P到a的距离，在平面图形PAQB中，有∠PAQ=∠PBQ=90°
∴P、A、Q、B四点共圆，且PQ是四边形PAQB的外接圆的直径2R
在△PAB中，∵PA=2，PB=2，∠BPA=180°-60°=120°，
由余弦定理得 AB²=4+4-2×2×2cos120°=12
由正弦定理：PQ=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4
∴点P到直线a的距离为4．

点评 本题中，通过作二面角的棱的垂面，找到二面角的平面角，属于中档题．