题目内容
3.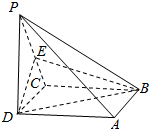 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.(1)证明:PA∥平面EDB;
(2)证明:平面PAC⊥平面PDB.
分析 (1)欲证PA∥平面EDB,根据直线与平面平行的判定定理可知只需证PA与平面EDB内一直线平行,连接AC,交BD于O,连接EO,根据中位线定理可知EO∥PA,PA?平面EDB,EO?平面EDB,满足定理所需条件;
(2)证明AC⊥平面PBD,即可证明平面PAC⊥平面PDB.
解答  证明:(1)设AC与BD相交于点O,则O为AC的中点.
证明:(1)设AC与BD相交于点O,则O为AC的中点.
∵E是P的中点,∴EO∥PA
又∵EO?平面EDB,PA?平面EDB,
∴PA∥平面EDB;
(2)∵PO⊥平面ABCD,∴PD⊥AC
又∵四边形ABCD为正方形,∴AC⊥BD
从而AC⊥平面PBD,
∴平面PAC⊥平面PBD.
点评 本题考查直线与平面平行的判定,以及平面与平面垂直的判定,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.在棱长为1的正方体ABCD-A1B1C1D1中,B1点到平面ACD1的距离为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
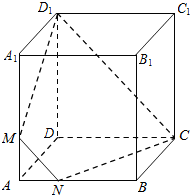 如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上
如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上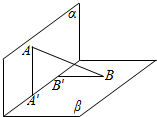 如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )