题目内容
(2007•河北区一模)如果方程
=kx恰有唯一解,则实数k的取值范围是
| |x-1| |
k∈(-∞,0]∪(
,+∞)
| 1 |
| 2 |
k∈(-∞,0]∪(
,+∞)
.| 1 |
| 2 |
分析:设y=
,y=kx,然后作出两个函数的图象,利用图象确定k的取值范围.
| |x-1| |
解答:解:y=f(x)=
,y=kx,则f(x)=
,图象关于x=1对称.
然后作出两个函数的图象,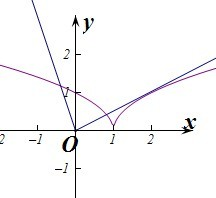
当k=0时,x=1,方程有一解,所以k=0成立.
当k≠0时,
由图象知当k<0时,两个方程恒有一个交点,成立.
当k>0时,当x>1时由kx=
,即k2x2=x-1,所以k2x2-x+1=0.
由△=0得,1-4k2=0,解得k=
,此时直线y=kx与f(x)相切,所以要使方程此时有唯一解,则k>
.
综上满足条件的k的取值范围是k∈(-∞,0]∪(
,+∞).
故答案为;k∈(-∞,0]∪(
,+∞).
| |x-1| |
|
然后作出两个函数的图象,

当k=0时,x=1,方程有一解,所以k=0成立.
当k≠0时,
由图象知当k<0时,两个方程恒有一个交点,成立.
当k>0时,当x>1时由kx=
| x-1 |
由△=0得,1-4k2=0,解得k=
| 1 |
| 2 |
| 1 |
| 2 |
综上满足条件的k的取值范围是k∈(-∞,0]∪(
| 1 |
| 2 |
故答案为;k∈(-∞,0]∪(
| 1 |
| 2 |
点评:本题主要考查函数与方程的关系,利用数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目