题目内容
(本小题满分13分)
已知函数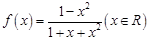 .
.
(Ⅰ)求函数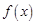 的极大值;
的极大值;
(Ⅱ)若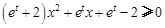 对满足
对满足 的任意实数
的任意实数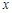 恒成立,求实数
恒成立,求实数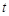 的取值范围(这里
的取值范围(这里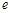 是自然对数的底数);
是自然对数的底数);
(Ⅲ)求证:对任意正数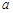 、
、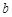 、
、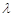 、
、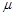 ,恒有
,恒有
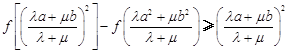
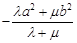 .
.
已知函数
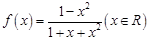 .
.(Ⅰ)求函数
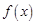 的极大值;
的极大值;(Ⅱ)若
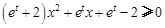 对满足
对满足 的任意实数
的任意实数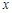 恒成立,求实数
恒成立,求实数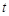 的取值范围(这里
的取值范围(这里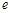 是自然对数的底数);
是自然对数的底数);(Ⅲ)求证:对任意正数
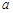 、
、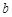 、
、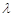 、
、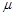 ,恒有
,恒有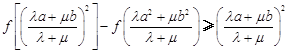
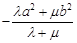 .
.(Ⅰ)极大值为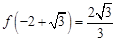 .(Ⅱ)
.(Ⅱ)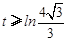 ;(Ⅲ)见解析。
;(Ⅲ)见解析。
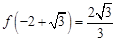 .(Ⅱ)
.(Ⅱ)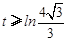 ;(Ⅲ)见解析。
;(Ⅲ)见解析。(Ⅰ)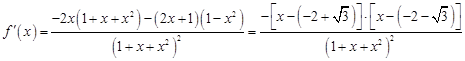
∴ 的增区间为
的增区间为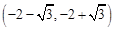 ,
,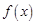 减区间为
减区间为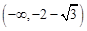 和
和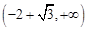 .极大值为
.极大值为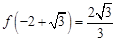 .
.
(Ⅱ)原不等式可化为 由(Ⅰ)知,
由(Ⅰ)知, 时,
时,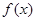 的最大值为
的最大值为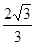 .
.
∴ 的最大值为
的最大值为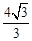 ,由恒成立的意义知道
,由恒成立的意义知道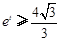 ,从而
,从而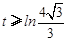
(Ⅲ)设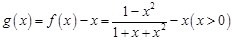
则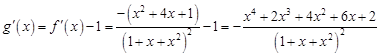 .
.
∴当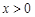 时,
时,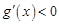 ,故
,故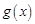 在
在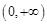 上是减函数,
上是减函数,
又当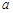 、
、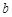 、
、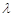 、
、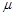 是正实数时,
是正实数时,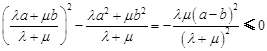
∴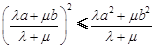 .
.
由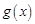 的单调性有:
的单调性有: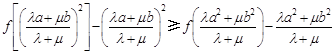 ,
,
即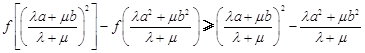 .
.
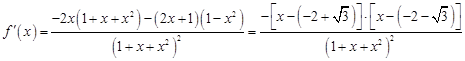
∴
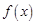 的增区间为
的增区间为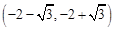 ,
,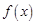 减区间为
减区间为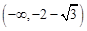 和
和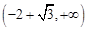 .极大值为
.极大值为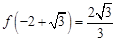 .
.(Ⅱ)原不等式可化为
 由(Ⅰ)知,
由(Ⅰ)知, 时,
时,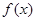 的最大值为
的最大值为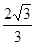 .
.∴
 的最大值为
的最大值为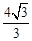 ,由恒成立的意义知道
,由恒成立的意义知道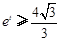 ,从而
,从而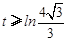
(Ⅲ)设
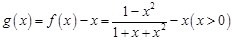
则
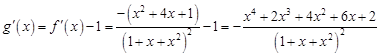 .
.∴当
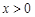 时,
时,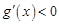 ,故
,故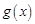 在
在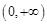 上是减函数,
上是减函数,又当
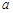 、
、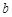 、
、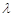 、
、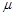 是正实数时,
是正实数时,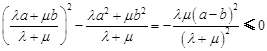
∴
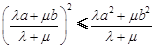 .
.由
 的单调性有:
的单调性有: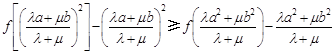 ,
,即
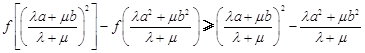 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的单调区间;
的单调区间;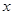 的方程
的方程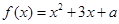 在区间
在区间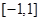 上有唯一实根,求实数
上有唯一实根,求实数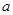 的取值范围.
的取值范围.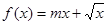 在区间
在区间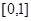 单调递增,则m的取值范围为
单调递增,则m的取值范围为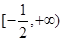
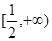
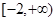
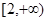
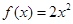 的图像上点P(1,2)及邻近点Q(
的图像上点P(1,2)及邻近点Q( ,
,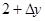 )则
)则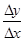 的值为
的值为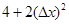
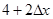
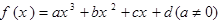 的对称中心为M
的对称中心为M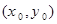 ,记函数
,记函数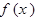 的导函数为
的导函数为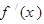 ,
, 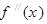 ,则有
,则有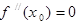 .若函数
.若函数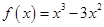 ,则可求得:
,则可求得: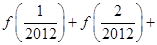
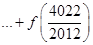
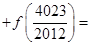 .
. ,其中
,其中 为正实数.
为正实数. 时,求
时,求 的极值点;
的极值点;
 为R上的单调函数,求
为R上的单调函数,求 附近的左侧
附近的左侧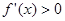 ,右侧
,右侧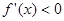 ,那么
,那么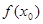 是极大值.
是极大值.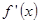 是函数
是函数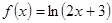 的导函数,则
的导函数,则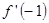 的值为 ( )
的值为 ( )