题目内容
.(本小题满分12分)
设 ,其中
,其中 为正实数.
为正实数.
(Ⅰ)当 时,求
时,求 的极值点;
的极值点;
(Ⅱ)若 为R上的单调函数,求
为R上的单调函数,求 的取值范围.
的取值范围.
设
 ,其中
,其中 为正实数.
为正实数.(Ⅰ)当
 时,求
时,求 的极值点;
的极值点;
(Ⅱ)若
 为R上的单调函数,求
为R上的单调函数,求 的取值范围.
的取值范围. (Ⅰ)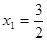 是极小值点,
是极小值点,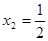 是极大值点.(II)a的取值范围是0<a≤1。
是极大值点.(II)a的取值范围是0<a≤1。
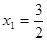 是极小值点,
是极小值点,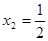 是极大值点.(II)a的取值范围是0<a≤1。
是极大值点.(II)a的取值范围是0<a≤1。本试题考查了导数在研究函数中的运用。
(1)根据已知函数求解定义域和导数,然后分析单调性,从而得到极值。
(2)因为 为R上的单调函数,则说明了
为R上的单调函数,则说明了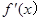 在R上不变号,由
在R上不变号,由 知,
知,
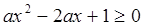 在R上恒成立,
在R上恒成立,
可知判别式小于等于零即可。
解:对 求导得
求导得 ①
①
(Ⅰ)当 ,若
,若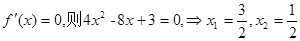
所以,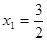 是极小值点,
是极小值点,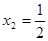 是极大值点.
是极大值点.
(II)若 为R上的单调函数,则
为R上的单调函数,则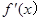 在R上不变号,由
在R上不变号,由 知,
知,
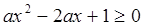 在R上恒成立,
在R上恒成立,
∴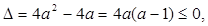 故
故
故a的取值范围是0<a≤1
(1)根据已知函数求解定义域和导数,然后分析单调性,从而得到极值。
(2)因为
 为R上的单调函数,则说明了
为R上的单调函数,则说明了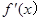 在R上不变号,由
在R上不变号,由 知,
知,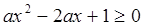 在R上恒成立,
在R上恒成立,可知判别式小于等于零即可。
解:对
 求导得
求导得 ①
①(Ⅰ)当
 ,若
,若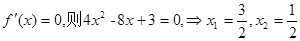
| x | 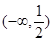 | 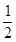 | 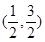 | 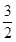 |  |
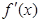 | + | 0 | - | 0 | + |
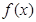 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以,
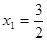 是极小值点,
是极小值点,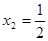 是极大值点.
是极大值点.(II)若
 为R上的单调函数,则
为R上的单调函数,则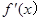 在R上不变号,由
在R上不变号,由 知,
知,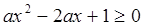 在R上恒成立,
在R上恒成立,∴
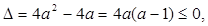 故
故
故a的取值范围是0<a≤1

练习册系列答案
相关题目
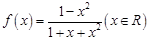 .
.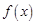 的极大值;
的极大值;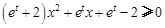 对满足
对满足 的任意实数
的任意实数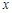 恒成立,求实数
恒成立,求实数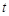 的取值范围(这里
的取值范围(这里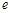 是自然对数的底数);
是自然对数的底数);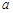 、
、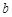 、
、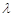 、
、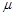 ,恒有
,恒有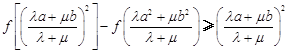
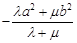 .
.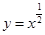 为导数的函数
为导数的函数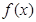 图象过点(9,1),则函数
图象过点(9,1),则函数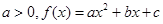 ,曲线
,曲线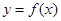 在点
在点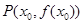 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为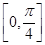 ,则点
,则点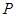 到曲线
到曲线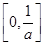
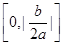
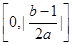
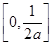

 的导函数
的导函数 .
.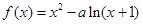 ,其中
,其中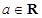 。
。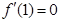 ,求a的值;
,求a的值;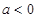 时,讨论函数
时,讨论函数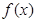 在其定义域上的单调性;
在其定义域上的单调性;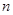 ,不等式
,不等式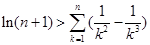 都成立。
都成立。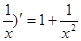
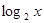 )′=
)′= 
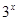 )′=
)′=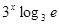
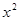 cosx)′=-2xsinx
cosx)′=-2xsinx 且
且 ,则
,则 ( )
( )



 则
则
